УДК I (091)
Игнатьев Михаил Борисович – федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный университет аэрокосмического приборостроения», доктор технических наук, профессор, директор Международного института кибернетики и артоники, Санкт-Петербург, Россия.
E-mail: ignatmb@mail.ru
190000, Санкт-Петербург, ул. Большая Морская, д. 67,
тел: 8(812)494-70-44.
Караваев Эдуард Федорович – федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный университет», доктор философских наук, профессор, профессор кафедры логики, Институт философии Санкт-Петербургского государственного университета, Санкт-Петербург, Россия.
E-mail: EK1549@ek1549.spb.edu
199034, С.-Петербург, Менделеевская линия, 5,
тел: +7-812-328-94-21, доб. 1844.
Авторское резюме
Задача исследования: Поначалу на земном шаре сложились цивилизации, которые были мало связаны друг с другом. В эпоху великих географических открытий их взаимодействия расширились, и в настоящее время современные средства транспорта и связи тесно объединили все страны мира, но возникли противоречия между самими странами. Глобализация стала разрушать сложившиеся культуры народов. Возникло мощное движение за многополярный мир. Президент России В. В. Путин неоднократно заявлял, что «если мы хотим, чтобы мир был безопасным, он должен быть многополярным».
Состояние вопроса: Практика международной политической жизни дает многообразный материал для анализа и осмысления. Но вполне очевидно, что без мощного информационного моделирования в этой области не обойтись. Использование компьютеров предполагает разработку языков различного уровня, позволяющих перейти с естественного языка разных научных дисциплин к языкам программирования. Весьма осложняющим фактором является всегда и всюду присутствующая в объективном мире и в сознании людей случайность.
Результаты: Для анализа и прогнозирования сложных ситуаций, возникающих в международных отношениях, достаточно эффективен метод лингво-комбинаторного моделирования, применяемый совместно со средствами современной символической логики (модальной, деонтической, временнóй) и теории вероятностей.
Ключевые слова: глобализация; социокультурный цикл; свойства сложных систем; национальные культуры; многополярный мир; проблемы устойчивого развития; лингво-комбинаторное моделирование; символическая логика; теория вероятности.
Problems of Sustainable Development of a Multipolar World in the Context of Globalization
Ignatyev Mikhail Borisovich – Saint Petersburg State University of Aerospace Instrumentation, professor, International Institute of Cybernetics and Artonics, director, Saint Petersburg, Russia.
E-mail: ignatmb@mail.ru
67, Bolshaya Morskaya st., Saint Petersburg, Russia, 190000,
tel: +7(812)494-70-44.
Karavaev Eduard Fedorovich – Saint Petersburg State University, Doctor of Philosophy, Professor, Department of Logic, Institute of Philosophy of Saint Petersburg State University, Saint Petersburg, Russia.
E-mail: EK1549@ek1549.spb.edu
5, Mendeleevskaya line, Saint Petersburg, 199034, Russia,
tel: + 7-812-328-94-21, ext. 1844.
Abstract
Research problem: At first on the globe, there appeared civilizations that had little to do with each other. In the era of great geographical discoveries, these interactions expanded, and now modern means of transport and communications have closely linked all the countries of the world, but there exist some contradictions between these countries themselves. The globalization began to destroy the existing cultures of peoples. A powerful movement for a multipolar world has emerged. Russian President Vladimir Putin has repeatedly stated: “If we want the world to be safe, it must be multipolar”.
The state of the question: The practice of international political life provides a variety of material for analysis and reflection. Nevertheless, it is obvious that we cannot do without a powerful information modeling in this area. The use of computers involves the development of languages at various levels, allowing the transition from the natural language of various scientific disciplines to programming languages. Chance, which is always and everywhere present in the objective world and in the consciousness of people, represents a very complicating factor.
Results: The authors suggest using the method of linguo-combinatorial modeling, together with the means of modern symbolic logic (modal, deontic, temporal) and of probability theory.
Keywords: globalization; socio-cultural cycle; properties of complex systems; national cultures; multipolar world; problems of sustainable development; linguo-combinatorial modeling; symbolic logic; probability theory.
Введение
Миллион лет назад медленно развивались первобытные общества, которые были очень устойчивыми образованиями. По мере развития технологий эти общества трансформировались, становились классовыми. В науке обозначилась тенденция, в которой постепенно отметалось как бы все ненужное из накопленного опыта человечества. Вновь возникающие общества становились все более неустойчивыми. По мнению К. Шмитта [см.: 1], в наше время сформировалась группа стран «цивилизации суши» и группа стран «цивилизации моря», которые имеют во многом противоположные интересы. Еще раньше Шмитт выдвинул идею «плюриверсума» – многополярного мира на планете [см.: 2; 7]. Сейчас существование многополярного мира стало общепризнанным фактом. По мере развития многополярного мира возродилось понятие устойчивого развития, которое в средние века понималось почти метафорически и обозначало возможность пройти как бы по тонкой грани между раем и адом. В настоящее время в рамках Организации Объединенных Наций сформировано уже две программы по устойчивому развитию [см.: 4; 5], и актуальным является системный анализ многополярного мира с точки зрения устойчивого развития, чему и посвящена настоящая статья.
1. Глобальный социокультурный цикл и глобализация
Экономика со времен Адама Смита существенно изменилась и представляет собой сложную самоорганизующуюся систему. После великих географических открытий XV–XVI веков в мире сложился глобальный социокультурный цикл [см.: 3; 6]. В наше время этот цикл охватывает все страны и регионы. Каждый человек может быть творцом в отдельный момент времени, творцы производят множество инноваций – проектов, патентов, песен и т. д. Эти инновации после апробации в микросредах, после прохождения цензуры попадают в средства массовой информации и обрушиваются на людей через телевидение, прессу, Интернет и вызывают по ассоциации у некоторых людей рождение новых идей, новых инноваций, и таким образом цикл повторяется многократно. Часть инноваций, проходя через конструкторские бюро (КБ) и различные производства, превращается в вещи – одежду, машины и т. п. – и опять-таки обрушивается потоком на людей и т. д. (см.: рис. 1). Этот социокультурный цикл является основой процессов глобализации, в которые погружено все человечество. Непрерывный поток инноваций в самых разных областях человеческой деятельности – неотъемлемый элемент современной картины мира и основа существования потребительского общества. Вместе с тем безудержное развитие потребительского общества ведет к исчерпанию природных ресурсов и росту социальных противоречий в обществе. Растет разница в доходах самых богатых и самых бедных слоев общества, самых богатых и самых бедных стран мира, что ведет к росту напряженности и терроризму. Необходимость международного регулирования этих проблем становится все очевиднее, что привело к рождению концепции устойчивого развития. Устойчивое развитие в русской транскрипции – это неточный перевод с английского слов «sustainable development», что означает поддерживающее развитие [см.: 4]. Этому термину много веков, в средневековой религиозной литературе он означал возможность пройти по тонкой грани между раем и адом.
Рисунок 1. Глобальный социокультурный цикл
В современном обществе большую роль играют деньги. Финансовый цикл оказывает большое влияние на экономику. Именно в финансовом цикле имело место массированное применение вычислительных систем и сетей. Если в 1950 году в торгах на биржах мира участвовали тысячи людей, то в 2000 году в торгах на биржах принимало участие свыше 100 миллионов человек через компьютерные сети. Изобретение кредитной карточки и развитие компьютерных сетей, которые связали магазины и банки, позволило ускорить оборот наличности в 10 раз. В настоящее время в виртуальном финансовом мире оборачивается гигантское количество денег, во много раз превосходящее валовой национальный продукт, что послужило источником многочисленных афер и спекуляций и вызвало в конце 2008 года мировой финансовый кризис. Создана международная информационно-вычислительная система расчетов SWIFT, с помощью которой США контролируют все расчеты во многих странах мира. Существует множество моделей социально-экономических процессов. Ниже рассматривается возможность их лингво-комбинаторного моделирования.
2. Лингво-комбинаторное моделирование слабо формализованных систем
Лишь для небольшого числа реальных систем имеются математические модели. Прежде всего, системы описываются с помощью естественного языка. Предлагается способ перехода от описания на естественном языке к математическим уравнениям. Например, пусть имеется фраза:
WORD1+WORD2+WORD3 (1)
В этой фразе мы обозначаем слова и только подразумеваем смысл слов. Смысл в представленной структуре естественного языка не отображен. Предлагается ввести понятие смысла в следующей форме:
(WORD1)*(SENSE1)+(WORD2)*(SENSE2)+(WORD3)*(SENSE3)=0 (2)
Будем обозначать слова как Аi от английского Appearance, а смыслы – как Еi от английского Essence, звездочка * означает операцию умножения. Тогда уравнение (2) может быть представлено как:
A1*E1+A2*E2+A3*E3=0 (3)
Уравнения (2) и (3) являются моделями фразы (1). Образование этих уравнений, приравнивание их к нулю есть операция поляризации.
Лингво-комбинаторная модель является алгебраическим кольцом (операторным кольцом), где используются три операции – сложение, вычитание и умножение – в соответствии с аксиомами алгебры, и мы можем разрешить уравнение (3) либо относительно Аi, либо относительно Еi путем введения третьей группы переменных – произвольных коэффициентов Us:
A1=U1*E2+U2*E3
A2=–U1*E1+U3*E3 (4)
A3=–U2*E1–U3*E2
или
E1=U1*A2+U2*A3
E2=–U1*A1+U3*A3 (5)
E3=–U2*A1–U3*A2,
где U1, U2, U3 – произвольные коэффициенты, которые можно использовать для решения различных задач на многоообразии (3). Если уравнения (4) или (5) подставить в уравнение (3), то оно тождественно обратится в нуль при любых Us. Впервые неопределенность была конструктивно введена в квантовой механике.
В общем случае, если имеем n переменных и m многообразий, ограничений, то число произвольных коэффициентов S будет равно числу сочетаний из n по m+1 [1]:
Это основной закон кибернетики. Число произвольных коэффициентов является мерой неопределенности и адаптивности (см.: таблица 1).
Таблица 1. Мера неопределенности и адаптивности
| n /m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | |||||||
| 3 | 3 | 1 | ||||||
| 4 | 6 | 4 | 1 | |||||
| 5 | 10 | 10 | 5 | 1 | ||||
| 6 | 15 | 20 | 15 | 6 | 1 | |||
| 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||
| 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |
| 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
Лингво-комбинаторное моделирование заключается в том, что в конкретной предметной области выделяются ключевые слова, которые объединяются во фразы типа (1), на основе которых строятся эквивалентные системы уравнений с произвольными коэффициентами. Лингво-комбинаторное моделирование включает все комбинации и все варианты решений и является полезным эвристическим приемом при изучении сложных систем. Таблица 1 иллюстрирует сдвинутый треугольник Паскаля, который связан с числами Фиббоначчи и Золотым сечением. Лингво-комбинаторный подход может быть распространен на моделирование многополярного мира.
3. Моделирование многополярного мира
Кризис капиталистического производства, свидетелями и участниками которого мы стали, заставляет задуматься о законах развития экономики. В учении Адама Смита о богатстве народов сказано: «Человек постоянно нуждается в помощи своих ближних, и тщетно было бы ожидать ее только от их благоволения. Он скорее достигнет своей цели, если призовет себе в помощь их эгоизм… Дай мне то, что мне нужно, и ты получишь то, что необходимо тебе…», ибо человек «…преследует собственную выгоду, причем в этом случае невидимой рукой направляется к цели, которая совсем не входила в его намерения». Все это хорошо, пока равнодействующая частных эгоизмов – она же невидимая рука рынка – выводит «в плюс». Сапожник тачает сапоги, пирожник печет пироги, сапоги и пироги обмениваются (скажем, на 1 сюртук и 20 аршин холста), богатство народов, направляемое «невидимой рукой», растет.
Во время кризиса, когда богатство народов рушится, сапожник и пирожник, а в еще большей степени кузнец и слесарь остаются без работы, ибо некому сбывать плоды своих трудов, гораздо реже слышны похвалы невидимой руке, хотя она никуда не делась. Равнодействующая частных эгоизмов действует – куда сложились векторы, туда и сложились, и случаются времена, когда все указанные Адамом Смитом предпосылки остаются в силе, богатство же народов не умножается, но идет в распыл. Невидимость руки рынка сохраняется – без войны, без чумы или землетрясения заводы, дороги, стройки обращаются в мерзость запустения, невидимая рука рынка превращается в когтистую лапу, и вся надежда – на человеческую солидарность и коллективизм. В рамках национальной солидарности от чистоты рыночных отношений остается немного. Например, протекционизм делается неизбежным в силу солидарности и осознания «свой своему поневоле брат». Заграница может поставить ряд товаров более дешевых и лучшего качества, но заграница не обещает кормить наших безработных и поддерживать нашу внутреннюю покупательную способность. Государство вынуждено вводить пошлины и поддерживать своего производителя. И еще острее стоит вопрос о законах развития социально-экономических систем, которые со времен Адама Смита существенно изменились.
Для примера проведем лингво-комбинаторное моделирование жизни города. Если в качестве ключевых слов взять «население», «пассионарность», «территория», «производство», «экология и безопасность», «финансы», «внешние связи», то в соответствии с вышеизложенной методикой уравнение города будет иметь вид:
А1*Е1+А2*Е2+…+А7*Е7=0, (7)
а эквивалентные уравнения будут иметь вид:
E1=U1*A2+U2*A3+U3*A4+U4*A5+U5*A6+U6*A7;
E2=–U1*A1+U7*A3+U8*A4+U9*A5+U10*A6+U11*A7;
E3=–U2*A1–U7*A2+U12*A4+U13*A5+U14*A6+U15*A7;
E4=–U3*A1–U8*A2–U12*A3+U16*A5+U17*A6+U18*A7; (8)
E5=–U4*A1–U9*A2–U13*A3–U16*A4+U19*A6+U20*A7;
E6=–U5*A1–U10*A2–U14*A3–U17*A4–U19*A5+U21*A7;
E7=–U6*A1–U11*A2–U15*A3–U18*A4–U20*A5–U21*A6,
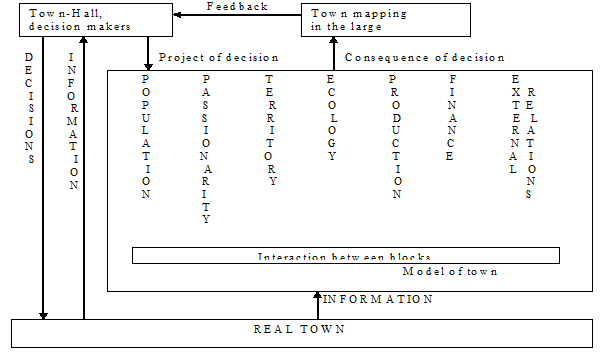
где А1 – характеристика населения, которая включает в себя характеристики здоровья, образования, занятости; А2 – характеристика пассионарности; устремлений групп населения, люди обладают свободой выбора при принятии решений, и этот выбор является важным, что оценивается путем социологического анализа; А3 – характеристика территории, включая наземные и подземные постройки, этот блок может быть геоинформационной системой; А4 – характеристика производства, включая оценку различных видов деятельности – научной, производственной, транспортной, торговой и др.; А5 – характеристика экологии и безопасности; А6 – характеристика финансов, финансовых потоков и запасов в городе; А7 – характеристика внешних связей города, включая оценку входящих и выходящих потоков людей, энергии, материалов, информации, финансов; Е1, …, Е7 – изменения этих характеристик соответственно; U1, U2, …, U21 – произвольные коэффициенты, которые могут быть использованы для управления и решения различных задач на многообразии (7). Наличие аналитической модели открывает возможность нахождения аттрактора каждого из городов или стран.
Рис. 2. Моделирование города для поддержки управленческих решений
Эта модель (рис. 2) используется в системах для поддержки принятия решений властями. Число блоков в лингво-комбинаторной модели города или страны может быть различным. С точки зрения точности моделирования, чем больше блоков используется, тем лучше, но при этом ухудшается наглядность модели, ее восприятие людьми, принимающими решение. Например, если население поделить на три блока – «дети и подростки», «взрослые» и «пенсионеры», то число переменных возрастет до девяти, уравнение города будет содержать девять переменных.
При моделировании города или страны важно рассматривать всю иерархию систем, из которых этот город или страна состоит. Главная ячейка – семья, для моделирования которой тоже можно использовать семиблочную модель, при этом будет изменяться содержание отдельных блоков. Любая семья имеет свое домашнее хозяйство, минимальный размер семьи – один человек, но и такая семья имеет все семь атрибутов. Аналогичным образом можно рассматривать другие семейные объединения – род, тейп, домен. Семиблочная модель может быть использована при моделировании различных предприятий, на которых работают люди, при этом структура блоков для каждого из типов предприятий будет разной. Однотипность модели, которая положена в основу моделирования и семьи, и предприятий, и районов, и города, и страны в целом, позволяет проще производить анализ и синтез сложных систем такого рода.
Развитие информационно-вычислительной техники позволяет поставить вопрос об обязательном предварительном моделировании последствий принимаемых решений, что позволит избежать многих ошибок.
С древнейших времен складывались способы управления коллективными работами и сообществами людей. Они базировались на введении правил взаимоотношения между людьми (правил этики, морали, заповедей, законов религии, в последующем – светских правил и правовых норм) и на создании иерархической системы управления с помощью административного аппарата. Но как отдельный человек, так и коллектив людей – это самоорганизующиеся системы, и различные способы управления – это различные методы внутреннего и внешнего управления самоорганизующейся системой. На уровне человека и социальных коллективов действуют факторы целеполагания и целеобразования.
4. Средства детализации и совершенствования лингво-комбинаторного моделирования с помощью инструментов современной символической логики
Способности системы к самоорганизации зависят от способности к целеполаганию, которая у различных людей разная. Бывают конформисты, которые готовы делать то, что делают другие, и даже готовы подчиняться целям других людей, особенно если эти цели выработал коллектив. Бывают личности с большой самостоятельностью мышления и сопротивляемостью навязываемым им мнениям. В зависимости от типа личности, менталитета народа люди могут стремиться формулировать цели единолично либо вырабатывать цели коллективно, что характерно для России.
У российского народа сложилось стремление к соборности, к коллективному принятию решений на сходах всех жителей деревни, на собраниях трудового коллектива предприятий, на советах различного рода. Способ управления, основанный на участии в целеобразовании активных элементов (человека, предприятия, региона и др.), является перспективным, несмотря на свою сложность. Не все люди способны к целеобразованию и стремятся участвовать в формулировании целей. Некоторые исследователи утверждают, что активных личностей в странах около 10 %, а большинство готово выполнять цели, поставленные руководством.
Различают следующие уровни целеобразования применительно к людям:
1) материальный, определяемый врожденными потребностями и программами человека (самосохранение, обеспечение питанием, минимумом одежды);
2) эмоциональный (доступные развлечения, эстетическое восприятие мира, проявление и реализация чувств любви, ненависти и др);
3) семейно-общественный (реализация программы продолжения рода, создания условий для воспитания потомства);
4) социально-общественный, определяемый правилами сообществ, закрепленных в законодательстве, этических нормах, традициях и т. п.;
5) интеллектуальный, для которого характерна система ценностей, ориентированная главным образом на развитие творческих способностей личности (примером может служить атмосфера академгородков в начальный период их развития).
В связи с развитием информационных технологий и виртуальных миров начинают выделяться два уровня: удовлетворения минимальных жизненных потребностей в реальном мире и в виртуальном мире, где человек сможет реализовать свои самые различные фантазии. Реализация этих уровней позволит смягчить гнет социального неравенства.
В материалах статистических бюро по городам и регионам и по странам в целом имеются почти все данные, необходимые для запуска модели. Другие данные, для оценки пассионарности, можно почерпнуть из социологических опросов.
К сожалению, для большинства задач имеется только формулировка на естественном языке, большинство задач плохо формализованы. Поэтому актуальным является переход от описания на естественном языке на язык основных соотношений, лингво-комбинаторное моделирование является одним из способов такой формализации.
Лингво-комбинаторное моделирование обеспечивает первоначальный переход с уровня языка той или иной научной дисциплины на языки различных уровней, связанные с составлением необходимых программ для обработки информации и перехода к информационному моделированию. Язык научной дисциплины можно, следуя выдающемуся специалисту в области теоретического и системного программирования, академику А. П. Ершову, назвать «языком научной прозы». Это, как мы знаем, – не то же самое, что естественный язык «в обычном понимании». С одной стороны, «язык научной прозы» «меньше» естественного языка в отношении использования риторических фигур, тропов и т. д. С другой стороны, он «больше» естественного языка на всякого рода символические конструкции (специальные термины, формулы и т. д.). Между уровнем собственно составления компьютерных программ, прохождение которых как раз и автоматизирует наши рассуждения, и «языком научной прозы» располагаются язык лингво-комбинаторного моделирования и его детализации. В них, в частности, уточняются представления о реальных людях и группах людей (малых и больших), которые действуют в реальном мире.
Названная детализация может быть осуществлена – в достаточно серьезном объеме – с помощью инструментов современной символической логики, на что авторы указывали уже достаточно давно [см.: 8–11].
Когда мы конкретизируем описания реальных процессов, действующими лицами которых являются люди, группы (малые и большие) людей, страны и государства и, наконец, народонаселение Земли в целом, мы используем соответствующие разделы современной символической логики. Это – алетическая модальная логика, которая позволяет уточнить отношение между необходимостью и случайностью; деонтическая логика, позволяющая уточнить ценностные аспекты сравниваемых альтернатив; временна́я логика, которая вводит временную квалификацию всех высказываемых суждений, и др. Следует также сказать о целесообразности использования в историческом исследовании и в прогнозировании и планировании инструментов теории вероятностей.
М. Блок, ещё один представитель школы «Анналы», пишет об этом так: «Историк, спрашивающий себя о вероятности минувшего события, по существу лишь пытается смелым броском мысли перенестись во время, предшествующее событию, чтобы оценить его шансы, какими они представлялись накануне его осуществления. Так что вероятность – все равно в будущем» [12] (см.: рис. 3).
Рис. 3. Схема рассуждений историка по М. Блоку
Не касаясь собственно логических выкладок, ограничимся пояснениями схемы хода рассуждений историка (и философа истории), каждая точка которой представляет собой то, что в семантике символической логики называется «возможным миром» (это – текущее, актуальное или возможное состояние мира). Если слева от точки ветвления используется выражение алетической модальной логики ╞□A, т. е. «необходимо, что A», то на всех ветвях справа выполняется ╞A, т. е. имеет место положение дел, описываемое высказыванием A. Если слева от точки ветвления используется выражение алетической модальной логики ╞◊A, т. е. «возможно, что A», то на некоторых ветвях справа выполняется ╞A, т. е. имеет место положение дел, описываемое высказыванием A. Если слева от точки ветвления используется выражение деонтической логики ╞OA, т. е. «обязательно, что A», то на всех ветвях справа выполняется ╞A, т. е. имеет место положение дел, описываемое высказыванием A. Если слева от точки ветвления используется выражение деонтической логики ╞PA, т. е. «разрешено (допустимо в нормативном смысле), что A», то на некоторых ветвях справа выполняется ╞A, т. е. имеет место, что положение дел, описываемое высказыванием A. Если слева от точки ветвления используется выражение временнóй ╞GA, т. е. «всегда будет так, что A», то на всех ветвях справа выполняется ╞A, т. е. имеет место положение дел, описываемое высказыванием A. И т. д. и т. п.
Покажем, какие возможности более адекватного и полного описания истории может обеспечить комбинирование средств модальной, деонтической и временнóй логики [13].
Вводим следующие определения.
Определение 1: положение дел, которое может быть создано или расстроено, предотвращено от наступления или от уничтожения (если оно уже имеет место), называется выполнимым состоянием.
Определение 2: положение дел называется выполнимым в прагматическом смысле, если его выполнение или невыполнение в заданных условиях может быть результатом человеческих действий.
Определение 3.1: подлинной нормой называется такая обязывающая норма, O-норма или разрешающая норма, P-норма, содержание которых является выполнимым в прагматическом смысле.
Определение 3.2: норма, содержание которой является необходимым или невозможным положением дел, называется неподлинной, или ложной.
Определение 4.1: множество O-норм является деонтически непротворечивым, если конъюнкция их содержаний, выражающая выполнимое состояние дел, является выполнимой в логическом смысле формулой.
Определение 4.2: каждое множество P-норм является деонтически непротворечивым.
В семантических исследованиях деонтической логики обычно используется “стандартная модель”: μ= 〈W, R, V〉. W является (непустым) множеством возможных миров, R – бинарное отношение деонтической альтернативности, а V – отображение из множества пропозициональных букв Var = {p0, p1, p2, …} в подмножества множества W.
Высказывание pi является истинным в возможном мире α, если и только α входит в подмножество wi, гдеwi есть результат отображения.
Естественным образом оценивание распространяется на применение деонтических операторов. Например, пусть OA обозначает «Обязательно, чтобы имело место состояние дел A»; тогда:
V(OA) = {α ∈ W: ∀β ∈ W(αRβ ⇒ β∈ V(A))}.
Учесть зависимость норм от времени позволяет временна́я логика. В нашем примере используем систему, в которой можно сравнивать времена событий, находящихся на различных «ветвях» множества возможных вариантов течения событий.
Базисное отношение предшествования определяется как степень элементарного отношения <’, которому присущи:
(i) иррефлексивность: ∀x¬(x <′ x)
(ii) единственность временного кванта: ∀x∀y(x <′ y → ¬∃z(x <′ z & z <′ y))
(iii) бесконечность: ∀x∃∀y(x <′ y) & ∀x∃y(y <’ x)
(iv) древовидность: ∀x∀y∀z(y <′ x & z <′ x → y = z)
(v) связность: ∀x∀y{x ≠ y → ∃z[∃v1∃v2 … ∃vn–1 (z <′ v1 & v1 <′ v2 &… & vn–1 <′ x) & ∃w1∃w2 … ∃wm–1 (z <′ w1 & w1 <′ w2 & … & wm–1 <′ y)]}.
Определение степени отношения <′ является таким:
(1) x <1 y, если и только если (еие) x <′ y
(2) x <n y, еие ∃v1∃v2 … ∃vn–1 (x <′ v1 & v1 <′ v2 & … & vn–1 <′ y).
Вводим также два условия:
(n+): между элементами базисного множества существует отношение только конечной (хотя и не ограниченной каким-либо конкретным числом);
(n++): Отсутствуют «петли»: ∀n(x <n y → x ≠ y).
Теперь вводим определение полного отношения на базисном множестве:
x < y iff ∃n (x <n y).
Ему присущи следующие свойства:
(i) иррефлексивность: ∀x ¬(x < x)
(ii) транзитивность: ∀x∀y∀z(x < y & y < z → x < z)
(iii) бесконечность: ∀x∃y(x < y) & ∀x∃y(y < x)
(iv) древовидность: ∀x∀y∀z(y < x & z < x → (y < z) ∨ (y = z) ∨ (z < y))
(v) связность: ∀x∀y(x ≠ y → ∃z(z < x & z < y))
(vi) дискретность:∀x[∃y(y < x) → ∃y(y < x & ¬∃z(y < z & z < x))] & ∀x[∃y(x < y) → ∃y(x < y & ¬∃z(x < z & z < y))].
Таким образом, мы используем модель времени ℑ b = 〈T, <〉, в которой базисное множество «моментов времени» T = {x, y, z, …} упорядочено бинарным отношением < «раньше-позже».
Мы используем следующие временные операторы:
F‘A для «Необходимо, что будет так, что A»;
F”A для «Необходимо, что в определённое время будет так, что A»;
G‘A для «Необходимо, что всегда будет так, что A»;
PA для «(Уже) было так, что A».
Теперь для возможных миров вводим отношение «исторического тождества»:
α ≅t β, если и только если α(t‘) = β(t‘) для каждого t‘< t
и отношение деонтической альтернативности релятивизируется по отношению ко времени:
Rt: если α Rt β, то α ≅t β.
Означивание является теперь таким:
Vt: если α(t) = β(t), то α ∈ wi (t), если и только если β∈ wi(t).
Мы получили овремененную модель μt = 〈Wt, Rt, Vt〉, где Wt есть декартово произведение множеств W и T, высказывания означиваются по отношению к парам 〈α, t〉, а выражение μt╞ A(α, t) обозначает «A является истинным в мире α во время t».
Условия истинности других формул релятивизируются по отношению к мирам и временам обычным образом. Например, для логических союзов:
μt╞ ¬A(α, t) еие не имеет места μt╞ A(α, t),
μt╞ (A → B) (α, t) еие не имеет места μt╞ A(α, t) или μt╞ B (α, t).
Для деонтических операторов:
μt╞ OA(α, t) еие ∀β ∈ Wt(α Rtβ ⇒ μtB A(β, t)).
Для временных операторов:
μt╞ HA(α, t) еие ∀t’∈ T(t’< t ⇒ μt╞ A(α, t’)),
μt╞ PA(α, t) еие ∃t’∈ T(t’< t & μt╞ A(α, t’)).
Можно ввести в язык два модально-временных оператора:
(1) «исторической необходимости» □t:
μt╞ □tA(α, t) еие ∀β ∈ Wt(α ≅t β ⇒ μt╞ A(α, t))
(2) и «исторической возможности» ◊t:
μt╞ ◊t A(α, t) еие ∃β ∈ Wt(α ≅t β & μt╞ A(β, t)).
Далее определим деонтически-временнóй оператор Ot:
Ot A = □t A ∨ □t ¬A.
Это – выражение исторической предопределенности: независимо от действий и усилий человека положение дел, описываемое с помощью данного высказывания A, выполняется или не выполняется в каждом мире из какого-то множества миров, которые имеют одну и ту же историю.
5. Совершенствование лингво-комбинаторного моделирования в отношении учета случайности во всем происходящем
Напомним, что в настоящее время вполне обосновано «избирательное сродство» теории вероятности и логики, т. е. возможность их совместного использования в составе единого исчисления с соблюдением всех необходимых синтаксических, семантических и прагматических стандартов [см.: 14].
Особенно важными в изучении случайности и адекватности её представления в современном научном познании являются результаты, полученные совместно работавшими на протяжении двух с лишним десятилетий (1972–1995) Д. Канеманом и А. Тверски [см.: 15], и результаты Н. Н. Талеба [см.: 16–18] (первое десятилетие текущего столетия).
Названными учеными на основе многочисленных эмпирических и теоретических исследований показаны удивительные ограничения нашего разума: чрезмерная уверенность в том, что́ мы будто бы знаем, и явная неспособность адекватно оценить «объем» нашего невежества. Осознавая время от времени неопределённость окружающего мира, мы, тем не менее, склонны переоценивать своё понимание мира и недооценивать роль случая в событиях. Чрезмерная уверенность «подпитывается» иллюзорной достоверностью оглядки на прошлое. Мы склонны переоценивать возможности наших инструментальных средств обращения со случайностью (скажем, марковские процессы или метод Монте-Карло), сами себя «одурачиваем» (выражение Талеба), полагая, что представленное в них понимание случайности адекватно охватывает объективную случайность. Талеб, – на наш взгляд, удачно – обратился к подзабытой метафоре «чёрного лебедя». Это – неожиданное (даже для эксперта в соответствующей области) событие со значительными последствиями; при этом, – в ретроспективе, – событие может быть вполне рационально объяснено, как если бы оно было ожидаемым. Заметим ещё, что есть не только «плохие» «чёрные лебеди», но и «хорошие» (неожиданная удача). Признавая всеобщность причинно-следственных связей, мы, естественно, и в статистическом материале ищем её проявления. Однако здесь мы сталкиваемся с серьёзными затруднениями. Канеман приводит следующий весьма типичный пример ошибочного умозаключения, связанного с оценкой случайности действительно случайных событий [15].
Последовательность появления на свет в больнице шести младенцев – мальчиков и девочек – является случайной: единичные события, составляющие событие – «шестёрку», являются независимыми, и число мальчиков и девочек, родившихся за последние часы, не влияет на пол следующего младенца. Теперь рассмотрим три возможные «шестёрки»: МММДДД, ДДДДДД, МДММДМ, где М обозначает рождение мальчика, а Д – девочки. Одинаковая ли у «шестёрок» вероятность? Поскольку события независимы, а варианты исхода Д и М примерно равновероятны, любая возможная последовательность полов шести новорожденных так же вероятна, как остальные. Обнаружив нечто, похожее на закономерность, мы отказываемся от мысли о случайности такого процесса. Канеман полагает – и нетрудно с ним согласиться, – что поиск причинно-следственных закономерностей унаследован нами от наших предков. Но это, очевидно, означает, что в нашем мышлении представления о случайности и причинно-следственной связи необходимо развивать дальше.
Кроме того, как отмечает Талеб, наш разум иногда «поворачивает стрелу причинности назад» [16]. Ведь из того, что каждый умный, трудолюбивый, настойчивый человек достигает успеха, не следует, что каждый успешный человек является умным, трудолюбивым и настойчивым! В приведённом примере имеет место элементарное логическое заблуждение и перемена местами антецедента и консеквента.
Возьмём пример несколько иного рода. М. Рейнор в книге «Парадокс стратегии» на основе аналитического обзора более чем тридцати эмпирических исследований и конкретного эмпирического материала, касающегося деятельности двух десятков с лишним ведущих компаний на протяжении двадцати лет, сформулировал достаточно неожиданное обобщение: «Стратегии, имеющие наибольшую вероятность успеха, имеют и наибольшую вероятность неудачи» [19]. Рейнор – на наш взгляд, справедливо, – указывает на то, что его вывод вовсе не оправдывает «ничего-неделание»: ведь это – тоже стратегия. Напротив, он напоминает мысль Луи Пастера: «Удача благоволит подготовленному уму, который её ищет».
Будущее является «открытым», неопределённым, непредсказуемым. Так что, формируя стратегию будущих действий, мы оцениваем их обстоятельства такими, какими они видятся нам сегодня.
Важнейшим метрическим средством в оценке роли случайности во всяком историческом процессе в настоящее время, несомненно, является гипотетико-дедуктивный метод в соединении с методом диагноза по Т. Байесу.
Предполагается, что у нас есть ряд гипотез: Н1, Н2, … , Нn. Известны априорные вероятности их наступления: Р(Н1), Р(Н2), … , Р(Нn). После некоторого количества опытов Е, мы меняем их на апостериорные вероятности: Р(Н1/Е), Р(Н2/Е), … , Р(Нn/Е).
Формула Байеса может рассматриваться как оптимальная модель для формулирования диагноза:
P(Hi/E) = P(Hi)۰ P(E /Hi)/ΣP(Hi)۰P(E/Hi), где P(E/Hi) = P(E۰Hi)/P(Hi);
P(Hi) ≠ 0, поскольку иначе Hi была бы невозможной; знак Σ указывает на суммирование от i = 1 до i= n.
Рассмотрим стандартный пример. Пусть у нас есть две непрозрачные урны. В одной (назовём её «красной») 70% красных шаров и 30% белых, в другой наоборот 30% красных шаров и 70% белых (её назовём «белой»). Посредством бросания монеты испытуемый выбирает одну из урн. Опыт состоит в том, что испытуемый посредством последовательности вытаскивания шаров из урны, установлением их цвета с возвратом в урну определяет, какая урна ему досталась.
Очевидно, в начале опыта: P0 (Hк) = P0(Hб) = 0,5. Воспользуемся приёмом Р. Джеффри [20]: будем использовать понятие «шансы» Ω, т. е. отношение вероятности благоприятных для данной гипотезы исходов опыта к вероятности неблагоприятных. Тогда:
P0(Hк) = P0(Hб) = 0,5 и
Ω0(Hк) = P0(Hк) / P0(Hб) = 1
P(Hк /E) = P0(Hк)∙P(E/Hк) / (P0(Hк)∙P(E/Hк) + P0(Hб)∙P(E/Hб))
P(Hб/E) = P0(Hб)∙P(E/Hб) / (P0(Hк)∙P(E/Hк) + P0(Hб)∙P(E/Hб))
Ω(Hк/E) = (P0(Hк) / P0(Hб))∙(P(E/Hк) / P(E/Hб)) = Ω0(Hк)∙ (P(E/Hк) /P(E/Hб)) = P(E/Hк) /P(E/Hб).
Исходом опыта E может быть либо вытаскивание «красного шара», либо «белого шара». Если E := красный шар, мы получаем; P(E/Hк) = 0,7; P(E/Hб) = 0,3 и Ω(Hк/E) = 7/3.
Если E := белый шар, получаем: P (E/Hк) = 0,3; P(E/Hб) = 0,7 и Ω(Hк/E) = 3/7.
Таким образом, если суммарный исход опыта EΣ есть, например, 12 вытащенных шаров, из которых 8 красных и 4 белых, мы получаем:
Ω(Hк/EΣ) = (7/3)8∙(3/7)4 = (7/3)8-4 = (7/3)4 ≈ 30.
Следовательно, шансы того, что испытуемому досталась «красная урна», в 30 раз больше того, что ему досталась «белая урна». А вероятность этого равна, соответственно, P(Hк/EΣ) = 30 / (1+30) ≈ 0,97.
Однако, возвращаясь к тому, что бывают «чёрные лебеди» и что не стоит самих себя «одурачивать», мы удерживаемся от абсолютизации метода Байеса: ведь всё равно и сейчас мы имеем дело не с объективной неопределённостью, а с нашими представлениями о ней.
6. Пример из современной ситуации
Сейчас «на слуху» кризис Европейского Союза. Почему разваливается Европейский Союз?
Любой союз накладывает дополнительные обязательства, ограничения. Как было показано выше, число произвольных коэффициентов в многомерных системах сначала растет, достигает максимума, а потом начинает убывать, это явление называется феноменом адаптационного максимума. История знает множество союзов, государств и империй, которые по разным причинам распадались, в том числе и потому, что правящие элиты не сумели удержать системы в зоне адаптационного максимума в потоке перемен. Такую ситуацию переживает в настоящий момент и Европейский Союз. Действительно, если число переменных союза n, а число ограничений m, то число произвольных коэффициентов в структуре эквивалентных уравнений будет вычисляться по формуле (6), и если каждый из 28 членов союза обладает адаптационными возможностями mi и ni, i = 1, 2,…,28 , то возможны два варианта: либо S больше суммы Si – и тогда союз возможен; либо S меньше суммы Si – и тогда союз может распасться, что мы и наблюдаем, то есть правящая элита союза не справилась с назначением необходимого число ограничений m и mi при заданном n. Таковы законы кибернетики, которые надо учитывать. Один из способов сохранить союз – это уменьшить или увеличить n. Будем наблюдать за перипетиями Европейского Союза.
Когда-то президент Франции Шарль де Голль предлагал создать объединение от Лиссабона до Владивостока. Президент Российской Федерации В. В. Путин в мае 2016 года развил это предложение, заявив о необходимости «…приступить к созданию на обширном пространстве от Атлантики до Тихого океана зоны экономического и гуманитарного сотрудничества, опирающегося на архитектуру равной и неделимой безопасности». Представляется интересным исследовать возможности этой зоны.
Заключение
Древнейшая книга – это «Китайская классическая книга перемен» [см.: 21], в которой утверждается, что мир непрерывно меняется. В нашу эпоху это видно отчетливо для каждого человека за время его жизни – с осознаваемого детства до взрослости и пенсионного возраста перемены отражаются в памяти конкретного человека и в памяти стран. Во многом стабильность многополярного мира определяется исторической памятью стран.
Список литературы
1. Schmitt C. Land und Meer. Eine Weltgeschichtliche Betrachtun. – Leipzig, 1942.
2. Schmitt C. Der Begriff des Plitisches. – Berlin, Duncker und Humbolt, 1932.
3. Моль А. Социодинамика культуры. – М.: Мысль, 1973. – 496 с.
4. Программа действий: «Повестка дня на XXI век» и другие документы конференции в Рио-де-жанейро / Сост. М. Китинг. – Женева: Центр «За наше общее будущее», 1993. – 69 с.
5. Преобразование нашего мира: повестка дня в области устойчивого развития до 2030 года // Резолюция Генеральной ассамблеи ООН 70/1, принятая 25.09.2015. – 2015. – 44 с.
6. Игнатьев М. Б. Кибернетическая картина мира. Сложные киберфизические системы. – СПб.: ГУАП, 2014. – 472 с.
7. Дугин А. Г. Теория многополярного мира.: – М.: Академический проект, 2015. – 358 с.
8. Игнатьев М. Б., Караваев Э. Ф. Моделирование физических структур и средства неклассической логики // Вычислительные процессы и структуры. Межвузовский сборник. Вып. 154. / Науч. ред. М. Б. Игнатьев. – Л.: ЛИАП, 1982. – С. 3–12.
9. Аристова М. В., Игнатьев М. Б., Караваев Э. Ф. Логика – необходимая часть инструментария искусственного интеллекта // Известия АН СССР. Техническая кибернетика. – 1983. – № 3. – С. 122–133.
10. Игнатьев М. Б., Караваев Э. Ф., Мясников В. А. Логика и формализованные аспекты искусственного интеллекта // ISAI. Международный симпозиум по искусственному интеллекту (Препринт). – Л.: АН СССР. Ленинградский институт ядерной физики им. Б. П. Константинова, 1983. – С. 1–13.
11. Ignatiev M. B., Karavaev E. F., Myasnikov V. A. Logic and Formalized Aspects of Artificial Intelligence // Artificial intelligence: Proceedings of International Federation of Automatic Control Symposium. – Oxford: Pergamon Press, 1984. – pp. 99–104.
12. Блок М. Апология истории, или Ремесло историка. – М.: Наука, 1973. – 232 с.
13. Karavaev E. F. (Ed. by Fr. Stadler, M. Stöltzner) A Deontic Logic with Temporal Qualification // Time and History. Proceedings of the 28 International Ludwig Wittgenstein Symposium. Kirchberg am Wechsel, Austria 2005. – Frankfurt et el.: Ontos Verlag, 2006. – pp. 459–467.
14. Караваев Э. Ф. «Избирательное сродство» теории вероятности и логики // Логика, язык и формальные модели. Сборник статей и тезисов участников Открытого Российско-Финского коллоквиума по логике – ORFIC-2012. – СПб.: СПбГУ, 2012. – С. 96–104.
15. Kahneman D. Thinking, Fast and Slow. – New York: Farrar, Straus and Giroux, 2011. – 500 p.
16. Taleb N. N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets. – New York: Random House, 2004. – xlviii + 320 p.
17. Taleb N. N. The Black Swan: The Impact of the Highly Improbable. – New York: Random House, 2007. – xxxiii + 445 p.
18. Taleb N. N. Antifragile: Things That Gain from Disorder. – New York: Random House, 2012. – xxi + 521 p.
19. Raynor M. E. The Strategy Paradox: Why Committing to Success Leads to Failure (And What to Do About It). – New York: Doubleday Books, 2007. – 320 p.
20. Jeffrey R. C. The Logic of Decision. – Chicago; London: University of Chicago Press, 1983. – pp. 164–183.
21. Китайская классическая книга перемен. ИЦЗИН / Сост. Ю. К. Шуцкий. – М.: Русское книгоиздательское товарищество, 1993. – 384 с.
References
1. Schmitt C. Land und Meer. Eine Weltgeschichtliche Betrachtun. Leipzig, 1942.
2. Schmitt C. Der Begriff des Plitisches. Berlin, Duncker und Humbolt, 1932.
3. Mol A. Social Dynamics of Culture [Sociodinamika kultury]. Moscow, Mysl, 1973, 496 p.
4. Keating M. (Comp.) The Programme of Action: “Agenda for the XXI Century” and other Documents of the Conference in Rio de Janeiro [Programma deystviy: “Povestka dnya na XXI vek” i drugie dokumenty konferentsii v Rio-de-zhaneyro]. Zheneva, Tsentr “Za nashe obschee buduschee”, 1993, 69 p.
5. Transforming our World: the 2030 Agenda for Sustainable Development. United Nations General Assembly Resolution A/RES/70/1 of 25 September 2015, 2015, 44 p.
6. Ignatyev M. B. Cybernetic Picture of the World. Complex Cyber-Physical Systems [Kiberneticheskaya kartina mira. Slozhnye kiberfizicheskie sistemy]. Saint Petersburg, GUAP, 2014, 472 p.
7. Dugin А. G. The Theory of a Multipolar World [Teoriya mnogopolyarnogo mira]. Moscow, Аkademicheskiy proekt, 2015, 358 p.
8. Ignatyev M. B., Karavaev E. F. Modeling of Physical Structures and the Means of Non-Classical Logic [Modelirovanie fizicheskikh struktur i sredstva neklassicheskoy logiki]. Vychislitelnye protsessy i struktury. Mezhvuzovskiy sbornik. Vypusk 154 (Computational Processes and Structures. Vol. 154), Leningrad, LIАP, 1982, pp. 3–12.
9. Аristova M. V., Ignatyev M. B., Karavaev E. F. Logic – Is a Necessary Tool of Artificial Intelligence [Logika – neobkhodimaya chast instrumentariya iskusstvennogo intellekta]. Izvestiya АN SSSR. Tekhnicheskaya kibernetika (Herald of the USSRAcademy of Sciences. Technical Cybernetics), 1983, № 3, pp. 122–133.
10. Ignatyev M. B., Karavaev E. F., Myasnikov V. А. Logic and Formalized Aspects of Artificial Intelligence [Logika i formalizovannye aspekty iskusstvennogo intellekta]. ISAI. Mezhdunarodnyy simpozium po iskusstvennomu intellektu (ISAI. International Symposium on Artificial Intelligence). Leningrad, АN SSSR; Leningradskiy institut yadernoy fiziki imeni B. P. Konstantinova, 1983, pp. 1–13.
11. Ignatiev M. B., Karavaev E. F., Myasnikov V. A. Logic and Formalized Aspects of Artificial Intelligence. Artificial intelligence: Proceedings of International Federation of Automatic Control Symposium, Oxford, Pergamon Press, 1984, pp. 99–104.
12. Block M. Apology of History or the Craft of the Historian [Apologiya istorii, ili remeslo istorika]. Moscow, Nauka, 1973, 232 p.
13. Karavaev E. F. (Ed. by Fr. Stadler, M. Stöltzner) A Deontic Logic with Temporal Qualification. Time and History. Proceedings of the 28 International Ludwig Wittgenstein Symposium, Kirchberg am Wechsel, Austria 2005. Frankfurt et el, Ontos Verlag, 2006, pp. 459–467.
14. Karavaev E. F. The “Elective Affinity” of Probability Theory and Logic [“Izbiratelnoye srodstvo” teorii veroyatnosti i logiki]. Logika, yazyk i formalnye modeli. Sbornik Otkrytogo Rossiysko-Finskogo kollokviuma po logike. ORFiC-2012 (Logic, Language and Computation. Collected Works and Theses of Participants of Open Russian Finnish Colloquium in Logic – ORFiC-2012). Saint Petersburg, SPbGU, 2012, pp. 96–104.
15. Kahneman D. Thinking, Fast and Slow. New York, Farrar, Straus and Giroux, 2011, 500 p.
16. Taleb N. N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets. New York, Random House, 2004, xlviii + 320 p.
17. Taleb N. N. The Black Swan: The Impact of the Highly Improbable. New York, Random House, 2007, xxxiii + 445 p.
18. Taleb N. N. Antifragile: Things That Gain from Disorder. New York, Random House, 2012, xxi + 521 p.
19. Raynor M. E. The Strategy Paradox: Why Committing to Success Leads to Failure (And What to Do About It). New York, Doubleday Books, 2007, 320 p.
20. Jeffrey R. C. The Logic of Decision. Chicago; London, University of Chicago Press, 1983, pp. 164–183.
21. Shutskiy Yu. K. (Comp.) Chinese Classical Book of Changes. I Ching [Kitajskaya klassicheskaya kniga peremen. ITSZIN]. Moscow, Russkoe knigoizdatelskoe tovarishhestvo, 1993, 384 p.
Ссылка на статью:
Игнатьев М. Б., Караваев Э. Ф. Проблемы устойчивого развития многополярного мира в условиях глобализации // Философия и гуманитарные науки в информационном обществе. – 2018. – № 2. – С. 25–46. URL: http://fikio.ru/?p=3180.
© М. Б. Игнатьев, Э. Ф. Караваев, 2018