УДК 167/168

 

Караваев Эдуард Федорович – федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный университет», доктор философских наук, профессор, профессор кафедры логики, Институт философии Санкт-Петербургского государственного университета, Санкт-Петербург, Россия.

E-mail: EK1549@ek1549.spb.edu

199034, Санкт-Петербург, Менделеевская линия, 5,

тел.: +7-812-328-94-21, доб. 1844.

Никитин Владислав Евгеньевич – федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный университет», кандидат философских наук, доцент, доцент кафедры онтологии и теории познания, Институт философии Санкт-Петербургского государственного университета, Санкт-Петербург, Россия.

E-mail: vladislav.nik@gmail.com

199034, Санкт-Петербург, Менделеевская линия, 5,

тел.: +7-812-328-94-21, доб. 1845.

Авторское резюме

Задача исследования: Показать, что появление компьютеров, машин нового типа, в которых главным является преобразование информации, делает возможным появление моделирования нового типа. В нём и модель, и среда представлены процессом прохождения компьютерной программы. Авторы статьи обращаются к мыслям К. Маркса о природе машин вообще, высказанным им 160 лет тому назад: «Это – созданные человеческой рукой органы человеческого мозга, овеществленная сила знания».

Состояние вопроса: Более 60 лет тому назад один из создателей кибернетики, У. Р. Эшби, охарактеризовал компьютеры как «усилители наших мыслительных способностей». Сущность компьютера представлена в «машине Тьюринга» (1936 г.), в специальном логико-математическом аппарате. В начале 1940-х гг. идея машины Тьюринга была материализована. Дж. фон Нейману компьютер обязан своей «архитектурой»: команды хранятся в том же запоминающем устройстве, где и символы, подлежащие преобразованиям. Информационное моделирование – это прохождение компьютерной программы. К. Э. Шеннон заложил основы теории информации (1948 г.). А. Н. Колмогоровым и американскими учёными Р. Соломоновым и Г. Чейтиным разработана алгоритмическая теория информации (конец 1960 гг.). К концу XX в. были выяснены физические ограничения, налагаемые на информационные процессы (работы Р. Ландауэра). Важные результаты, касающиеся влияния случайности на наше мышление, были получены во второй половине ХХ в. (Д. Канеман, А. Тверски, Н. Н. Талеб).

Результаты: Развитие идей К. Маркса о природе машины позволяет уяснить природу «информационного моделирования»: оно является «автоматизированным мысленным экспериментом». Далее следует обратиться к понятию «по-став» (нем. «Ge-Stell») и его информационному аспекту, на что фактически указывал сам М. Хайдеггер (1966 г.). Информационное моделирование позволяет уточнить «каналы», по которым случайность влияет на наше мышление. Существуют топологические средства, которые с ним в решении этой задачи продуктивно сочетаются. Это же относится и к важнейшему метрическому средству – гипотетико-дедуктивному методу, в соединении с диагнозом по Т. Байесу.

Выводы: Информационное моделирование с помощью компьютера представляет собой «автоматизированный мысленный эксперимент». В настоящее время он имеет важнейшее значение в теоретической и практической деятельности.

 

Ключевые слова: машина; компьютер; информационное моделирование; случайность; многообразие; формула Байеса.

 

The Nature of Information Modeling and Its Actuality

 

Karavaev Eduard Fedorovich – Saint Petersburg State University, Doctor of Philosophy, Professor, Department of Logic, Institute of Philosophy of Saint Petersburg State University, Saint Petersburg, Russia.

E-mail: EK1 549@ek1549.spb.edu

5, Mendeleevskaya line, Saint Petersburg, 199034, Russia,

tel.: + 7-81 2-328-94-21, ext. 1844.

Nikitin Vladislav Evgenievich – Saint Petersburg State University, Ph. D. (Philosophy), Associate Professor, Department of Ontology and Theory of Knowledge, Institute of Philosophy of Saint Petersburg State University, Saint Petersburg, Russia.

E-mail: vladislav.nik@gmail.com

5, Mendeleevskaya line, Saint Petersburg, 199034, Russia,

tel.: + 7-81 2-328-94-21, ext. 1845.

Abstract

Research aim: To show that the emergence of computers, machines of a new type, in which the main thing is the transformation of information, makes possible the emergence of a new type of modeling. In this case, the computer program passage represents both the model and the environment. The authors of the article refer to Karl Marx’s thoughts about the nature of machines in general, which he expressed 160 years ago: “These are the organs of the human brain created by the human hand, the reified power of knowledge”.

Background: More than 60 years ago, one of the creators of cybernetics, William R. Ashby characterized computers as “amplifiers of our mental abilities”. The essence of the computer is represented in the “Turing machine” (1936), in a special logical-mathematical apparatus. In the early 1940s, the idea of the Turing machine was materialized. The computer owes its ‘architecture’ to John von Neumann: commands are stored in the same storage device as the symbols to be converted. Information modeling is the passage of a computer program. C. E. Shannon laid the foundations of information theory (1948). A. N. Kolmogorov and American scientists R. Solomonoff and G. J. Chaitin developed algorithmic information theory (late 1960s). By the end of the XX century physical limitations imposed on information processes had been clarified (R. Landauer’s works). Important results concerning the influence of chance on our thinking were obtained in the second half of the twentieth century (D. Kahneman, A. Tversky, N. N. Taleb).

Results: The development of Karl Marx’s ideas about the nature of the machine allows us to understand the essence of “information modeling”. This modeling consists in the computer program passage, and this is an “automated thought experiment”. One should also turn to the concept of “Ge-Stell” and its information aspect, which M. Heidegger himself actually pointed out (1966). Information modeling makes it possible to clarify the “channels” through which chance affects our thinking. There are topological tools, which are productively combined with it in solving of this problem. The same is true to the most important metric tool – hypothetical-deductive method, in conjunction with the diagnosis according to T. Bayes.

Conclusion: Computer-assisted information modeling is an “automated thought experiment”. Currently, this method is essential for theoretical and practical activities.

 

Keywords: machine; computer; information modeling; chance; manifold; Bayes’ formula.

 

Введение

Наука о компьютерах и их применениях, или информатика – одна из наиболее развивающихся и влияющих на познание и практику дисциплин. Один из создателей кибернетики, английский учёный Уильям Росс Эшби уже более шестидесяти лет тому назад назвал компьютеры «усилителями наших мыслительных способностей» [28]. Они позволяют производить громоздкие расчёты, решать сложные системы уравнений, выполнять поиск логического вывода, доказывать теоремы[1] и – может быть, самое впечатляющее – строить и изучать модели (в виде компьютерных программ) для объектов, являющихся предметами фактически любых областей науки и практической деятельности.

 

Создавать «усилители мыслительных способностей» люди пробовали давно. Так, в XIII в. Раймундом Луллием было построено механическое логическое устройство, получившее название «луллиевой машины» и позволявшее осуществлять силлогистические умозаключения [см.: 20, с. 132–133][2].

 

Компьютер – это машина. Так что целесообразно обратиться к мыслям К. Маркса о природе машины, высказанным 160 лет тому назад [17, с. 215]: «Природа не строит ни машин, ни локомотивов, ни железных дорог, ни электрического телеграфа, ни сельфакторов, и т. д. Все это – продукты человеческого труда, природный материал, превращенный в органы человеческой воли, властвующей над природой, или человеческой деятельности в природе. Все это – созданные человеческой рукой органы человеческого мозга, овеществленная сила знания».

 

Сейчас трудно представить, как появление машин нового типа отразится на работе самого нашего мозга. В качестве аналогии можно вспомнить изобретение пишущей машинки (1867 г.). Ф. Ницше, начавший пользоваться ею из-за болезни глаз, отметил: «Пользоваться пишущей машинкой поначалу утомительнее всякого писания» [19, c. 447]. Он даже сделал обобщение, кажущееся верным, – что «все пишущие инструменты влияют на наши мысли» [41, p. 23].

 

Мы, очевидно, уясняем природу «усилителей мыслительных процессов», только если сосредотачиваемся на том, что происходит с информацией. При этом важно принимать во внимание то, до какой глубины мы различаем информационные процессы. С этой точки зрения от «луллиевой машины», продуманной до уровня субъектно-предикатной структуры суждения, до современных компьютеров, продуманных на уровне элементарных символов («0» и «1») – «дистанция огромного размера».

 

Практические разработки и теоретические исследования в области информатики ведутся взаимосвязано. Но здесь нет «равномерности», «синхронности» и т. п. Скажем, «вдруг» усилиями Джорджа Буля появляется мощнейший аппарат («булева алгебра»), который и делает возможным развитие логических основ информационного моделирования. Машина Чарльза Бэббеджа по своим практическим возможностям в роли «усилителя мыслительных способностей» не идёт ни в какое сравнение с современными компьютерами. Но, располагая такой машиной, Ада Лавлейс построила язык программирования. И всё-таки, повторим, наука о компьютерах, или информатика – дисциплина нашего времени.

 

Машина Тьюринга

Природа компьютера представлена в «машине Тьюринга» [см.: 69], предложенной А. М. Тьюрингом в начале 1936 г.[3] Показательно, что этот аппарат является одновременно и предметом теоретического исследования, и методом обращения с символическими конструкциями (знаковыми моделями).

 

Машина Тьюринга полностью удовлетворяет требованиям к машинам, выполняющим алгоритмы:

(а) она является полностью детерминированной и действует строго в соответствии с заданной системой правил;

(б) она допускает ввод различных «начальных данных» (соответствующих задаче из заданного класса задач);

(в) система правил и класс решаемых задач так согласованы друг с другом, что всегда можно «прочитать» результаты работы машины.

 

Кратко напомним описание архитектуры машины Тьюринга.

 

(1) Имеется неограниченно длинная одномерная лента, которая разбита на ячейки. В каждой ячейке может быть записан только один символ х из некоторого конечного алфавита Х; при этом в алфавит входит и пустой символ.

 

(2) В каждый момент времени на ленте имеется только конечное (хотя и как угодно большое) количество непустых ячеек.

 

(3) Имеется специальная считывающая и записывающая головка, которая может либо перемещаться вдоль ленты вправо или влево на одну ячейку за один такт работы, либо оставаться на месте.

 

(4) Имеется некоторый конечный автомат А; у него конечное число внутренних состояний Q = {q₀, q₁, q₂….q_n-1}, и он работает в дискретном времени t = 0, 1, 2, …

 

Входом машины является элемент из множества X; выходом – элемент из множества {( Х Ä М )Èстоп}, где Х Ä М – декартово произведение множеств Х и М; М = {Л, П, Н}, Л – сдвиг головки влево, П – сдвиг головки вправо, Н – головка остаётся на месте; если выходом является стоп, то машина останавливается.

 

Функция переходов автомата a: если автомат находился в состоянии q_j и воспринимал вход x_i, то он переходит в состояние q_k= a (q_j, x_i).

 

Функция выходов автомата d: для той же пары áq_j, x_i ñ в ячейку, напротив которой находилась головка, записывается символ x_k = a (q_j, x_i); при этом x_i и x_k могут совпадать; а в зависимости от того, чему равно m из множества М, головка сдвинется влево, или вправо, или останется на месте. При выходе стоп, машина останавливается, и такие состояния (их может быть несколько) называются «состояниями покоя».

 

Имеются средства для композиции машин Тьюринга: умножение, возведение в степень, итерация. Они позволяют из одних машин Тьюринга (более простых) строить другие. Есть универсальные машины Тьюринга: они позволяют моделировать работу любой машины Тьюринга.

 

Знаменитый тезис Тьюринга, или тезис Тьюринга-Чёрча можно сформулировать так [8; 9]: «Неформальное (интуитивное) понятие эффективной процедуры над последовательностью символов совпадает с точным (формальным) определением понятия процедуры над (этой же) последовательностью символов, которая может быть выполнена на машине Тьюринга».

 

Этот тезис, так сказать, «вечная гипотеза». Его нельзя доказать строго формально: для этого пришлось бы дать строго формальное определение «интуитивного» (!). Он был бы опровергнут, если бы удалось указать такую процедуру, которая была бы признана эффективной в интуитивном смысле, а затем доказать, что эта процедура не может быть выполнена ни на какой машине Тьюринга. Уверенность в справедливости этого тезиса основана на том, что до сих пор дело обстоит так: если удаётся установить существование некоторой эффективной, в интуитивном смысле, процедуры, то удаётся построить такую машину Тьюринга, которая воспроизводит эту процедуру.

 

Появление компьютеров и информационного моделирования

В начале 1940-х гг. идея машины Тьюринга была материализована. В этом участвовал и сам Тьюринг, а также другие математики, физики, представители технических и технологических дисциплин, инженеры. Особо следует упомянуть Дж. фон Неймана, которому, в первую очередь, компьютеры обязаны своей «архитектурой»: ему принадлежит остроумная идея хранить команды, т. е. правила преобразования символов, в том же запоминающем устройстве, где хранятся и сами символы, подлежащие преобразованиям.

 

Информационное моделирование, которое мы здесь рассматриваем (его иногда называют «симулированием», перенося английское слово в русский язык), относится к тому типу моделирования, когда и модель, и среда являются искусственными: это – прохождение компьютерной программы. Для его философского осмысления целесообразно использовать хайдеггеровское понятие «по-став» (нем. «Ge-Stell») [25, c. 229], выделяя его информационное измерение, на что сам М. Хайдеггер фактически и указал в интервью журналу «Der Spiegel» (1966 г.) [1, c. 245; 39, p. 278].[4] Таким образом, с появлением компьютеров в научной картине мира, во взаимодействии человечества и мира информационное измерение начинает играть важную роль, не «заслоняя», разумеется, материального и энергетического измерений.

 

Информационные процессы, протекающие в компьютере, связаны и с природой материальных носителей, и с природой соответствующих энергетических преобразований. Более того, как мы знаем сейчас – об этом мы будем говорить далее подробнее – существуют определённые количественные соотношения между тремя компонентами: материальным, энергетическим и информационным – в любом объекте.

 

Носители информационных процессов в поколении компьютеров, предшествующем нынешнему поколению, были электромеханическими.[5] Были и есть проекты использовать в той же роли лазерные процессы, сложные химические соединения вроде молекул ДНК. Природа используемого носителя, естественно, влияет на форму информационных процессов, или на их «внешние характеристики»: скорость выполнения операций, объём запоминающих устройств и др. В той мере, в какой форма любого объекта связана с его содержанием, такого рода характеристики носителя информации влияют на содержание информационных процессов.[6]

 

Говорить более определённо о влиянии материального воплощения на информационные процессы сейчас не приходится. Представляется также, что нельзя согласиться и с утверждением, что вообще не имеет значения, каково материальное воплощение информационных процессов в компьютере [см.: 60].

 

Так или иначе, «до поры до времени» в наших теоретических размышлениях в области информатики мы не принимали во внимание тот факт, что реальные информационные процессы связаны с использованием реальных материальных (в первую очередь, физических) и энергетических возможностей. А они определяются объективными (физическими) законами.[7]

 

Конструкторы компьютеров в своей работе опираются на знания о физических свойствах используемых материалов и о законах, которым подчиняются процессы, протекающие в этих материалах, для того, чтобы обеспечить подходящие характеристики элементов компьютеров: надёжность выполнения простейших операций, сокращение времени их выполнения, уменьшение интенсивности неизбежного рассеяния энергии («информационное трение»).

 

Вопрос о том, каковы реальные диапазоны параметров и процессов, происходящих в компьютерах, напоминает ситуацию, имевшую место в середине XIX века, когда с появлением паровых двигателей возник вопрос о параметрах соответствующих материальных и энергетических процессов.[8]

 

Стремление улучшить рабочие характеристики реальных паровых машин инициировало открытие и формулирование второго начала термодинамики – одного из фундаментальных законов действительности. Можно предполагать, что определение фундаментальных ограничений параметров информационных процессов, протекающих в компьютерах, приведёт к открытиям такой же значимости.

 

Теория информации

«Информационной реальностью» мы называем определённые материальные образования искусственного происхождения, «артефакты», и те технологии, т. е. явления и процессы, которые имеют в них место. Сущность названных процессов и явлений состоит в создании, переработке, хранении и передаче информации, предназначенной для управления и регулирования человеческой деятельностью самого разнообразного характера – как той, которую мы называем «физической деятельностью», так и той, которую мы называем «умственной деятельностью»[9].

 

Как известно, научное понятие информации начало разрабатываться не так давно – в конце первой половины ушедшего столетия: в 1948 г. К. Э. Шеннон опубликовал работу (статью из двух частей), в которой были изложены основные положения теории информации [см.: 27; 63; 64]. Его величайшая научная заслуга состоит в том, что он сформулировал критерий, который позволяет сравнить количества информации, содержащиеся в сообщениях. Иначе говоря, он предложил способ измерения информации.

 

Разработанная Шенноном теория оперирует только вероятностями сообщений (или исходов рассматриваемых опытов) и полностью отвлекается от собственно содержания этих сообщений (исходов). Количество информации, содержащейся в сообщении x, определяется так: I(x) = – log₂P(x), где x – сообщение, Р(x) – его вероятность.[10]

 

Эта концепция имеет дело только с техническими (технологическими) проблемами без учёта смысла и ценности содержания сообщений, без анализа семантических и многих прагматических проблем. Но достаточно помнить, что изучение технической стороны информационных процессов является только первым, начальным, этапом, который, будучи совершенно необходимым, разумеется, не является последним. Никто и ничто не обязывает нас им ограничиваться. Вместе с тем ясно также, что мы не можем передавать наши мысли с должной точностью по системе, которая передаёт символические (языковые) конструкции, представляющие наши мысли, неточно. Овладеть сначала технической стороной информационных процессов – это вполне рациональный шаг, шаг на пути нашего познания информационной реальности – так сказать, определённого «среза» всей реальности и, прежде всего, «артефактизированной» реальности.[11]

 

Развитие теории информации

Шенноном заложены основы теории информации, и всякие последующие разработки будут включать в себя то, что он сделал, в качестве необходимой части. Алгоритмическая теория информации была разработана А. Н. Колмогоровым и американскими учёными Р. Соломоновым и Г. Чейтиным в конце 1960-х гг. Центральным понятием теории является «колмогоровская сложность».

 

Колмогоров хотел уточнить в теории вероятностей понятие случайной последовательности символов. Соломонов занимался разработкой индуктивного вывода с учётом знаменитого принципа, называемого «бритвой Оккама» [см.: 65]. Чейтин изучал программную сложность машин Тьюринга. Колмогоров, продвигаясь в своих исследованиях, пришёл к уточнению понятия информационного содержания последовательности символов. Чейтин последовал за ним и принял его подход. Появилась алгоритмическая теория информации [см.: 31].

 

Неформально «колмогоровскую сложность»[12] данной последовательности из нулей и единиц можно определить как длину самой короткой программы, которая может породить эту последовательность [см.: 12; 13].

 

Длины всех знаковых последовательностей – они, естественно, могут описывать любые объекты – измеряются в битах. Описание бинарной последовательности s – это просто программа, написанная как строка из определённого количества битов, которая производит последовательность s как результат. Принимая во внимание все возможные программы, которые генерируют данную последовательность s, и выбирая самую короткую, мы получим минимальное описание последовательности s, обозначаемое как d(s).

 

Если существует более одной программы одинаковой длины, то в качестве d(s) выбирается первая из множества таких программ, упорядоченного лексикографическим образом. Итак, «колмогоровская сложность» последовательности двоичных символов s есть длина минимального описания K(s), и K(s) = | d(s) |.[13]

 

Информационное содержание последовательности двоичных символов x определяется как её «колмогоровская сложность» I(x). Суммарная информация I(x, y) двух последовательностей x и y определяется, соответственно, как самая короткая программа, которая позволяет получить их обеих. Условная, или соотносительная информация I(x/y) последовательности x, вычисленная при условии, что определена информация последовательности y, определяется как длина самой короткой программы, которая позволяет вычислить x из y. Последовательности, которые могут выводиться короткими программами, рассматриваются как не очень сложные.

 

Выяснилось, что данный подход эффективен и может быть использован для постановки и доказательства невозможности некоторых результатов – таких, например, как доказательство – аналог теоремы Гёделя о неполноте или проблема останова («зависания») машины Тьюринга.[14] Кроме того, оказывается, что не имеет принципиального значения выбор языка программирования.

 

Энергетические ресурсы в информатике

К концу ушедшего столетия весьма основательно были выяснены физические ограничения, налагаемые на информационные процессы [см.: 55].[15]
Зададимся вопросом: каким количеством информации двое участников могут обменяться через данный канал связи при условии, что заданы определённые энергетические ресурсы? С одной стороны, квантовая механика ограничивает физические ресурсы любой системы в отношении её способности хранить, передавать и обрабатывать информацию [см.: 57]. С другой стороны, общая теория относительности ограничивает количество информации, которая может храниться в конечном объёме пространства в соответствии с термодинамикой «чёрных дыр» [см.: 27].

 

В исследование фундаментального, микрофизического уровня организации современной информационной реальности, связанной с использованием компьютеров, внёс существенный вклад американский ученый Рольф Ландауэр. Его концепция с философской точки зрения проста, и в то же время в техническом отношении она тщательно проработана им самим и его последователями (а также и оппонентами) в области физики и информатики.

 

Несколько нестрого он заявляет, что «информация является физической». Означает это заявление – как можно видеть из содержания его работ [см.: 43–52] – что информация не является какой-то абстрактной и ни во что не воплощённой сущностью. Она всегда предполагает некоторого рода материальную репрезентацию той или иной природы (знаки на бумаге, гравировка на каменной плите, спин элементарной частицы, заряд и др.). Это связывает процессы обработки и передачи информации со всеми возможностями и ограничениями конкретного материального (физического) уровня бытия, физическими законами и наличным, конечным в области нашего человеческого обитания, запасом материальных (физических) ресурсов. Так что, заимствуя терминологию из информатики, можно сказать на самом деле: нет программного хозяйства (англ. software) в смысле какой-то воплощённой в материальном субстрате информации (англ. hardware).

 

Процессы обработки и передачи информации зависят от того, что является возможным с материальной, физической точки зрения, что имеется в существующих видах вещества и полей, и от того, каково содержание физических законов. Природные, физические законы определяют направления, формы и способы обработки информации, что представлено в алгоритмах. Напомним, что алгоритм является артефактом; так что если он работает, то это означает, что нет никаких противоречий между его компонентами и связями между ними, с одной стороны, и законами природы, с другой.

 

Ландауэр несколько иронически замечает, что подчас физики «индоктринированы» пониманием величин математиками: «При условии, что задана бесконечно малая величина ε, (существует) такое N, что …», где N – как угодно (т. е. неограниченно) большое число». Но разве можно уверенно утверждать, что подразумеваемая этим как угодно большим N как угодно продолжительная неограниченная последовательность безошибочных операций в действительности выполнима?

 

Достаточно ли наличных степеней свободы, которые можно совместно увязать в каком-то компьютере,[16] для того чтобы у нас была возможность вычислить число π с любой желательной точностью? В реальном мире имеют место проблемы, связанные с «неидеальностью» и износом всякого оборудования. Разумно ли предполагать, что они могут быть решены с любой желательной точностью? И если нет, то это означает, что, например, привычный для нас в сугубо теоретических областях чистой математики числовой континуум не имеет непосредственного отношения к исполняемым на реальных компьютерах реальным алгоритмам и к реальным физическим законам. Так что алгоритмы, которые являются выполнимыми, в действительности, в реальном мире, необходимо должны соответствовать тем законам, которые в нём действуют.

 

Конечно же, утверждение о том, что «информация является физической», не означает, что математика и информатика являются «частями» физики. Однако это утверждение является вполне продуктивным философско-научным принципом – в свете изложенного истолкования и понимания того, что не бывает и не может быть информационных процессов без материальных процессов, связанных с носителями сигналов, и без необходимых энергетических затрат.

 

Говоря о генезисе этого принципа, можно напомнить достаточно давно (1934 г.) высказанные мысли лауреата Нобелевской премии П. У. Бриджмена, связанные с его попыткой справиться с парадоксами теории множеств [см.: 30]. Если внимательно сопоставить мысли Ландауэра и мысли Бриджмена о том, каковы «пожелания» физиков в отношении математического аппарата, с точки зрения его соответствия описанию конкретных, т. е. конечных фрагментов реального мира, то мы увидим, что речь у них идёт об одном и том же. Они оба не разделяют мнение многих (но не всех!) математиков о том, что канторова теория множеств в её современном виде (предусматривающем, заметим, современное представление классической логики) способна играть роль интуитивно приемлемой основы разнообразных областей математики, в том числе и математического анализа, используемого физиками (Бриджмен), и языков программирования различного уровня, использующихся в информатике (Ландауэр). В первую очередь, это представления о «бесконечных совокупностях одновременно существующих объектов» и «уровень согласованности» принимаемых идеализаций с результатами опытного (экспериментального) исследования природы на макро-, микро- и мегауровнях детализации и «охвата» в пространстве-времени.[17]

 

Ландауэр рассказывает, что именно статья Бриджмена послужила одним из источников его концепции [см.: 45]. Эта статья под выразительным названием «Реакция физика на теорию множеств по зрелом размышлении» [30] была опубликована в журнале, который ориентировался на освещение фундаментальных вопросов математики. При этом редактор журнала сделал оговорку, что, печатая интересную статью профессора П. У. Бриджмена, журнал, как и в случае всех статей вообще, просит не понимать факт публикации в журнале как признание того, что статья выражает точку зрения редакции. Как комментирует эту оговорку Ландауэр, по прошествии многих десятилетий можно только гадать о том, какие чувства испытывал редактор математического журнала, помещая статью известного учёного-физика, чтобы не обидеть его, и опасаясь недовольства читателей-математиков. Бриджмен, подчёркивает Ландауэр, возражал против расплывчатых, самореференциальных определений в обосновании теории множеств и предлагал использовать процедуры, в которых каждый шаг мог бы выполняться непосредственно и недвусмысленно.

 

Можно присоединиться к положительной оценке Ландауэром хода мыслей Бриджмена от критики указанных недостатков в обосновании теории множеств в направлении к концепции «потенциальной осуществимости». Можно также согласиться с предположением Ландауэра о том, что Бриджмен был бы вполне удовлетворён ограничением математики до того, что может быть выполнено на машине Тьюринга, которая, кстати сказать, вскоре (1936 г.) и появилась. В самом деле, интересно и совпадение с современной практикой употребление Бриджменом термина «программа» для обозначения последовательности чётких инструкций. Но – как, на наш взгляд, совершенно правильно отмечает Ландауэр – мы не находим у Бриджмена продолжения в виде постановки вопроса о физической реализуемости этих инструкций, что является принципиальным для концепции Ландауэра. Представляется только гадать, что было бы, если бы Бриджмен когда-нибудь вернулся к обсуждению рассматриваемой темы. Скажем, если бы он принял участие в обсуждении природы машины Тьюринга, то стал бы он задавать, например, такие вопросы: «Насколько реалистично предположение о неограниченной длине рабочей ленты машины?», «Предоставляет ли наша вселенная достаточно возможностей для этого?», «И если мы создадим в достаточном количестве оборудование для выполнения очень точных и надёжных вычислений, то не будет ли это оборудование вызывать своё собственное физическое воздействие на окружение?»

 

Таким образом, Ландауэр, «отталкиваясь от» размышлений Бриджмена, представляет свою основную идею о зависимости характеристик информационных процессов от физических законов, которым подчиняются существующие виды вещества и полей в более общем виде. В функционировании машины Тьюринга и в строении алгорифмов – если они работают и если мы хотим, чтобы они работали – непременно присутствуют характеристики реального мира[18].

 

Идеи Ландауэра, естественно, распространяются и на процессы коммуникации. Чтобы линия связи действовала, энергия не должна рассеиваться [см.: 51]. Однако на кодирование информации в той или иной среде нужна энергия – даже и в том идеализированном случае, когда мы считаем, что шумы отсутствуют. Посредством увеличения количества привлекаемой энергии можно получить более высокую скорость передачи информации. Но существуют ограничения на пропускную способность канала R. В самом деле, будем предполагать, что информация кодируется и «укладывается» в некоторые «порции» материала с массой покоя r, которые посылаются со скоростью v. Пусть «порции» настолько плотно заполнены, что используются все имеющиеся в нашем распоряжении степени свободы для хранения информации. При передаче, в соответствии со специальной теорией относительности, «порция» длиной покоя L будет сжиматься в продольном направлении в соответствии с известным преобразованием Лоренца g. Время между двумя последовательными «порциями» равняется τ = L / (g×v). Скорость передачи информации задаётся посредством: R = I/τ, где I – информация (т. е. энтропия для того случая отсутствия шумов, который мы рассматриваем), содержащаяся в «порции».

 

Чтобы определить максимально возможную величину I, используется «предел Бекенштейна», ограничивающий информацию, которая может храниться в сферическом объёме пространства с определённым радиусом на объекте с заданной энергией покоя [см.: 29]. «Предел Бекенштейна» связан с «принципом неопределённости» Гейзенберга: существуют верхние пределы для количества различных квантовых состояний и для скорости, с которой могут происходить изменения состояний. Другими словами, принцип неопределённости устанавливает верхний предел на плотность информации системы. Эта величина составляет: S £ A / 4, где S – энтропия, A – планковская площадь, т. е. площадь двухмерной области, имеющей радиус, равный планковской длине.

 

При её расчёте предполагается, что количество физических полей ограничено и что имеет место линейность определённого рода, в смысле отсутствия взаимодействия между различными видами полей. Кроме того, приведённые соображения, как на это указывают сами учёные [см.: 57], не применимы к гравитационному полю. Они не применимы также к неупорядоченным системам, в которых движение является диффузионным, а не баллистическим. Однако, остроумно замечают учёные, было бы крайне удивительным, если бы беспорядок позволял более эффективный способ передачи информации.

 

Примеры применения алгоритмической теории информации

В «Рассуждении о метафизике» Лейбница можно прочесть: «Предположим, например, что кто-нибудь сделал бы на бумаге множество точек наугад… Я утверждаю, что можно найти геометрическую линию, понятие о которой будет постоянным и единообразным соответственно некоторому правилу, и линия эта пройдёт через все точки и в том же самом порядке, как их набросала рука. Если бы кто-нибудь начертил сходу линию, которая была бы то прямою, то шла по окружности или ещё как-нибудь, всегда можно было бы найти понятие, или правило, или уравнение, общее всем точкам этой линии, в соответствии с которым должны произойти отмеченные изменения в направлении… Но когда правило слишком сложно, тогда то, что соответствует ему, считается неправильным» [14, с. 129–130].

 

По-видимому, следует присоединиться к интерпретации и развитию мыслей Лейбница, принадлежащим одному из создателей алгоритмической теории информации Чейтину [см.: 34], а именно: можно провести различие между такими фактами, которые возможно описать посредством некоторого закона, и такими фактами, которые являются незакономерными, нерегулярными. Лейбниц фактически говорит, что теория должна быть проще, чем описание тех фактов, на которых она основана и которые (в первую очередь) она объясняет; в противном случае она не объясняет ничего, является «неправильной».

 

Понятие «закон» становится бессодержательным, если при его формулировании допускается какая угодно математическая сложность. В самом деле, в этом случае всегда можно предложить формулировку – независимо от того, насколько случайными и нерегулярными являются исходные данные. Наоборот, если одна-единственная возможная формулировка желаемого закона для какого-то множества фактов является чрезвычайно сложной, то эти данные в действительности не охватываются законом. Соответственно, понятие «теория» становится бессмысленным, если допускается как угодно большая сложность теории: ведь в этом случае всегда имеется какая-то «теория».

 

Эта идея разработана с помощью алгоритмической теории информации и понятия «колмогоровской сложности»: описание данных и изложение содержания теории после составления соответствующих программ предстают в цифровой форме, а затем можно сравнить две полученные последовательности (объёмы программ) по количеству битов друг с другом.

 

Итак, важнейшее наблюдение Лейбница можно сформулировать более точно. Для любого конечного множества фактов всегда существует теория, которая является в точности такой же сложности, в точности таких же размеров в битах, как и сами факты. Она просто непосредственно выдаёт их «как они есть», не делая никакого вычисления. Но это не даёт нам возможности различать то, что мы можем понять, и то, что не можем, потому что всегда существует теория, которая является такой же сложной, как и то, что она объясняет.

 

При прочих равных условиях теория, взятая в качестве объяснения, является удачной только до такой степени, до которой она сжимает количество двоичных цифр, содержащихся в представлении фактов, в намного меньшее количество двоичных цифр, содержащихся в представлении теории. В некотором смысле, понимание является сжатием, постижение есть сжатие! Именно так мы можем выразить различие между настоящими теориями и ad hoc теориями.[19]

 

Понятие колмогоровской сложности и алгоритмическая теория информации позволяют уточнить понятие случайной последовательности символов [см.: 33]. Это в определённом смысле помогает нам лучше понять содержание категории «случайность».

 

Существует так называемый «парадокс случайности». Пусть заданы две последовательности, составленные и символов «0» и «1», по двадцать элементов в каждой из них, причём элементы обеих получены посредством бросания монеты:

х = 00000000000000000000

у = 01001110100111101000

 

Согласно теории вероятностей, эти последовательности имеют одинаковую вероятность ((1/2)²⁰). Однако «интуитивно» мы не воспринимаем х как случайно построенную последовательность: в ней слишком отчётливо присутствует регулярность. В то же время у предстаёт как по-настоящему нерегулярная, случайная последовательность: соседние элементы последовательности «0» или «1» появляются на основании того или иного результата бросания монеты, а не на основании какой-то взаимозависимости их, коренящихся непосредственно в последовательности.

 

Напомним характеристику случайности, данную Гегелем: «Мы… рассматриваем случайное как нечто такое, что может быть и может также и не быть, которое может быть таким, а также и другим, чьё бытие или небытие, бытие такого или другого рода имеет своё основание не в нём самом, а в другом» [4, с. 243].

 

Алгоритмическая теория информации позволяет выявить указанное различие с помощью оценки сложности программы для машины Тьюринга. Конечная последовательность квалифицируется как случайная, если её колмогоровская сложность (длина программы) примерно равна длине её самой, т. е. если мы не можем построить более короткую программу.

 

Заметим, что ещё имеется зависимость длины программы от выбора способа кодирования и языка программирования; так что, вообще говоря, конечная последовательность может быть случайной в одном случае – так сказать, «в одной системе отсчёта» – и не быть таковой в другом случае («в другой системе отсчёта»).

 

Чейтин дал ещё одно определение: бесконечная последовательность символов является случайной, если сложность, связанная с объёмом программы для продуцирования некоторого начального отрезка последовательности, имеющего длину n, не может быть сделана как угодно меньше п.

 

Было бы преувеличением считать, что приведённые математические факты совершенным образом обеспечивают «полную» экспликацию содержания категории случайности [34], как это, по-видимому, считает сам Чейтин. Но следует также отметить и то, что Чейтин добросовестно квалифицирует традицию, которую он продолжил как лейбницевскую.

 

В самом деле, в 1673 г. Лейбниц демонстрировал в Лондонском королевском обществе, членом которого его избрали, одну из первых вычислительных машин (усовершенствованную машину Блеза Паскаля). Он же одним из первых оценил достоинства двоичного исчисления и тот факт, что описание чего угодно может быть выполнено посредством использования только «0» и «1». Наконец, метод формализации как универсальный метод современной науки тоже разрабатывался Лейбницем. В одной из современных работ, принадлежащей перу одного из крупнейших учёных в этой области Мартина Дэвиса, Лейбниц назван «первым учёным в области информатики» [38].

 

Тогда же Чейтин впервые представил своё знаменитое число Ω, которому позже посвятил много публикаций, в том числе добротную монографию [34]. Это – вероятность останова универсальной машины Тьюринга U, т. е. вероятность того, что U остановится при условии, что на её вход подаются «0» или «1», выбираемые по результатам бросания монеты – для того, чтобы на выходе получать элементы последовательности W. Очевидно, получаемая бесконечная последовательность является случайной в глубоком смысле слова.

 

В самом деле, двоичные цифры («0» и «1») числа W являются, так сказать, «математическими фактами», которые оказываются таковыми не в силу какого-то обоснования: нет обоснования, которое было бы по своему объёму в битах меньше, чем они сами. Так что нарушается принцип достаточного основания Лейбница, «в силу которого … ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым без достаточного основания» [15]. Но в математике основанием того, что нечто является истинным, является доказательство. А двоичные цифры величины W являются такими-то и такими-то не в силу какого-либо основания: мы не можем установить, какими являются их значения.

 

Но, как на это указывает сам Лейбниц в параграфах 33 и 35 «Монадологии» [см.: 16], доказательство относительно сложного утверждения состоит в том, что мы посредством анализа его, посредством разбора его, сводим его истинность к истинности утверждений, которые являются настолько простыми, что они не требуют никакого доказательства большей длины (самоочевидные аксиомы). Но это означает, что в данном случае у нас доказательства нет. Равным образом, поскольку всё что угодно можно доказать из принципов, которые являются в равной степени сложными, например, посредством присоединения подлежащего доказательству утверждения к заданной системе в качестве новой аксиомы, постольку от такого «доказательства» пользы мало. И это – именно ситуация, которая имеет место с двоичными цифрами величины Ω.

 

Информационное моделирование и уточнение «каналов» влияния случайности на наше мышление

Информационное моделирование позволяет реализовать вполне определившийся интерес современной методологии социально-гуманитарных наук более адекватно и полно учитывать роль «всепроникающей», повсюду и всегда присутствующей случайности. Особенно важными в оценке того, как велико влияние случайности на наше мышление, являются результаты, полученные совместно работавшими на протяжении двух с лишним десятилетий (1972–1995 гг.) Д. Канеманом и А. Тверски [см.: 7; 44], и результаты, полученные Н. Н. Талебом и опубликованные в первом десятилетии текущего столетия [см.: 21; 22; 23; 66; 67; 68]. В этих работах убедительно показано, как мы, «одурачивая самих себя», подменяем нашими средствами репрезентации случайности (так сказать, «рандомизации в широком смысле слова») самоё объективную случайность.

 

Авторы статьи ранее уже высказывали свои соображения по поводу подхода к уточнению «каналов», по которым случайность влияет на наше мышление [см.: 10; 11]. Ими предлагается использовать некоторые топологические н метрические средства. Прежде всего, это понятие «многообразие»[20], которое ввёл Б. Риман ещё в 1854 г. [см.: 18]. Его унаследовал Э. Гуссерль в понятии «жизненный мир». В 1883 г. он защитил на философском факультете Венского университета диссертацию (первую) на математическую тему по вариационному исчислению. Думается, что это «волшебное слово» (по выражению Г.-Г. Гадамера) генетически связано со зрелым этапом биографии Гуссерля, а оно из той же парадигмы, что и «многообразие».

 

В своём рассмотрении возможностей как максимально более систематического и полного учёта случайности в нашем воображении и в конструировании образа мира авторы статьи используют понятие «многообразие» в качестве общенаучного понятия. Так что любой реальный объект – как материальной, так и идеальной природы – можно считать «многообразием», а взаимодействие объектов, соответственно – отображением одного «многообразия» на другое.

 

Понятие «многообразие» лежит в основе концепции «многомерного интеллекта» Г. Гарднера (1983 г.) [см.: 3]. Согласно этой концепции, наш разум является «многомерным» (“multiple”), и можно выделить 7 основных измерений разума:

(1) языковое;

(2) логико-математическое;

(3) визуальное;

(4) звукомузыкальное;

(5) телесно-кинестетическое;

(6) внутриличностное;

(7) межличностное.

 

Названные измерения являются характеристиками единого целого – многомерного разума. При этом они являются ортогональными, т. е. такими, что никакое измерение не сводится к какому-либо другому измерению или к нескольким другим.

 

Каждый человек характеризуется уникальным сочетанием различных более или менее развитых измерений разума, чем и объясняются индивидуальные различия между людьми. Способности людей различных культур представляют собой различные комбинации тех или иных видов интеллекта. Так мы можем отметить один из уровней проявления случайности.

 

Далее, мы обращаемся к принципам «димензиональной онтологии» В. Э. Франкла (1965 г.) [см.: 24]. Они позволяют проследить отображение одного многообразия в другом.

 

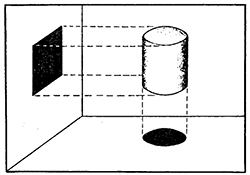
Первый принцип: один и тот же объект (цилиндр), проецируемый из его «жизненного» пространства» с бόльшим числом измерений (=3) в «познавательное пространство» субъекта с меньшим числом измерений (=2), может продуцировать различные предметы (круг, прямоугольник).

 

Рис.1. – Первый принцип В. Франкла

 

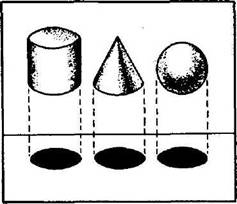
Второй принцип: различные объекты, проецируемые из их (общего) «жизненного пространства» с бόльшим числом измерений (=3) в «познавательное пространство» субъекта с меньшим числом измерений (=2), могут продуцировать одинаковые предметы (круг, круг, круг).

 

Рис.2. – Второй принцип В. Франкла

 
Описанные топологические средства продуктивно сочетаются с логико-математическими языками и языками программирования, используемыми в информационном моделировании.

 

Важнейшим метрическим средством в оценке роли случайности в нашем мышлении является, по мнению авторов, гипотетико-дедуктивный метод в соединении с методом диагноза по Т. Байесу.

 

Мы предполагаем, что у нас есть ряд гипотез: Н₁, Н₂, … , Н_n. Известны априорные вероятности их наступления: Р(Н₁), Р(Н₂), … , Р(Н_n). После некоторого количества опытов Е, мы меняем их на апостериорные вероятности: Р(Н₁/Е), Р(Н₂/Е), … , Р(Н_n/Е).

 

Формула Байеса может рассматриваться как оптимальная модель для формулирования диагноза:

P(H_i/E) = P(H_i)۰ P(E /H_i)/ΣP(H_i)۰P(E/H_i), где P(E/H_i) = P(E۰H_i)/P(H_i);

P(H_i) ≠ 0, поскольку иначе H_i была бы невозможной; знак Σ указывает на суммирование от i = 1 до i= n.

 

Однако, разумеется, мы удерживаем себя от абсолютизации и метода информационного моделирования, и метода Байеса по той «простой» причине, что всё равно и здесь мы имеем дело не с объективной случайностью как таковой, а с нашими представлениями о ней.

 

Заключение: об одном важнейшем применении информационного моделирования

Стоит напомнить, что в феврале 2004 г. на физическом факультете СПбГУ состоялась встреча учащихся и сотрудников с выпускниками Университета, академиками Р. И. Илькаевым (выпуск 1961 г.) и Ю. А. Трутневым, выпуск (1950 г.) – руководителями РФЯЦ-ВНИИЭФ РАН (г. Саров). Они рассказали, что в 1953 г. А. Д. Сахаров совершил «прорыв» в области создания ядерного оружия для укрепления обороноспособности нашей Родины. В 1990 г. Советский Союз предложил установить мораторий на ядерные испытания, который был согласован с Великобританией и США. Это создало возможность продвинуться по пути всестороннего запрета на проведение всех ядерных испытаний. Как известно, Договор о всеобъемлющем запрещении ядерных испытаний был подписан в 1996 г.

 

Тем не менее, как известно, изобретенное А. Д. Сахаровым оружие претерпевает модернизации. Но ни одного «натурного испытания», т. е. эксперимента, не производится. А как же судить о совершенствовании оружия? Посредством информационного моделирования, т. е. построения и «прогона» соответствующих компьютерных программ, описывающих процессы ядерного взрыва (с учетом обновления конструкции оружия).

 

Физики как естествоиспытатели, вполне понимая, что это в основном способ придания самим себе чувства более непосредственного, так сказать, «материального», контакта с физической реальностью, параллельно используют моделирование ядерного взрыва с помощью лазерных процессов.

 

Список литературы

1. Беседа сотрудников журнала «Шпигель» Р. Аугштайна и Г. Вольфа с М. Хайдеггером 23 сентября 1966 г. // Философия Мартина Хайдеггера и современность. – М.: Наука, 1991. – С. 233–250.

2. Булос Дж., Джеффри Р. Вычислимость и логика. – М.: Мир, 1994. – 400 с.

3. Гарднер Г. Структура разума: теория множественного интеллекта. – М.: ООО «И. Д. Вильямс», 2007. – 512 с.

4. Гегель Г. В. Ф. Энциклопедия философских наук. Часть первая. Логика // Гегель. Соч. – Т. I. – М. – Л.: Государственное издательство, 1929. – 368 с.

5. Гомер. Илиада. (V 785–786.) // Гомер. Илиада. Одиссея. – М.: Государственное издательство «Художественная литература», 1967. – 767 с.

6. Звонкин А. К., Левин Л. А. Сложность конечных объектов и обоснование понятия информации и случайности с помощью теории алгоритмов // Успехи математических наук. – Т. 25. – Вып. 6. – М.: Изд-во АН СССР, 1970. – С. 85 – 127.

7. Канеман Д. Думай медленно … решай быстро. – М.: АСТ, 2014. – 654 с.

8. Караваев Э. Ф. Современные рассмотрения тезиса Черча-Тьюринга // Вестник Санкт-Петербургского университета. Серия 6: Философия, политология, социология, психология, право. – 1996. – Вып. 2 (№13). – С. 28–33.

9. Караваев Э. Ф. Формализация – инструмент, разрабатываемый логикой для научного познания // Вестник Санкт-Петербургского университета. Серия 6: Философия, политология, социология, психология, право. – 1999. – Вып. 2 (№13). – С. 3–10.

10. Караваев Э. Ф., Никитин В. Е. Топологические и метрические средства учёта случайности в социокультурном анализе технологического развития // Контуры будущего: технологии и инновации в культурном контексте. Коллективная монография. Под ред. Д. И. Кузнецова, В. В. Сергеева, Н. И. Алмазовой, Н. В. Никифоровой. – СПб.: Астерион, 2017. – С. 113–116.

11. Караваев Э. Ф., Никитин В. Е. Синергетическая философия истории, случайность, логика, время // Философия и гуманитарные науки в информационном обществе. – 2018. – № 1 (19). – С. 12–32. – [Электронный ресурс]. – Режим доступа: http://fikio.ru/?p=3088 (дата обращения 30.09.2018).

12. Колмогоров А. Н. Три подхода к определению понятия «количество информации» // Проблемы передачи информации. – Т. 1. – №1. – М.: Наука, 1965. – С. 3–11.

13. Колмогоров А. Н. К логическим основам теории информации и теории вероятностей // Проблемы передачи информации. – Т. 5. – №3. – М.: Изд-во АН СССР, 1969. – С. 3–7.

14. Лейбниц Г.-В. Рассуждение о метафизике // Лейбниц Г. В. Соч.: В 4-х т. Т.1. – М.: Мысль, 1982. – С. 125–163.

15. Лейбниц Г.-В. Начала природы и благодати, основанные на разуме // Лейбниц Г.-В. Соч.: В 4-х т. Т.1. – М.: Мысль, 1982. – С. 404–412.

16. Лейбниц Г.-В. Монадология // Лейбниц Г.-В. Соч.: В 4-х т. Т.1. – М.: Мысль, 1982. – С. 413–439.

17. Маркс К. Экономические рукописи 1857-1859 годов. // Маркс К., Энгельс Ф. Сочинения. Т. 46. Ч.II. Изд. 2-е. – М.: Политиздат, 1968. – 618 с.

18. Риман Б. О гипотезах, лежащих в основании геометрии // Риман Б. Сочинения. – М.-Л.: ОГИЗ, Государственное издательство технико-теоретической литературы, 1948. – С. 279–293.

19. Сафрански Р. Ницше: биография его мысли / Р. Сафрански; пер. с нем. И. Эбаноидзе. – М.: Издательский дом «Дело» РАНХиГС, 20l6. – 456 с.

20. Стяжкин Н. И. Формирование математической логики. – М.: Наука, 1967. – 508 с.

21. Талеб Н. Одураченные случайностью. Скрытая роль шанса в бизнесе и жизни. – М.: Манн, Иванов и Фербер. 2011. – 320 с.

22. Талеб Н. Н. Черный лебедь. Под знаком непредсказуемости. – М.: КоЛибри, Азбука-Аттикус, 2011. – 528 с.

23. Талеб Н. Н. Антихрупкость. Как извлечь выгоду из хаоса. – М.: КоЛибри, Азбука-Аттикус, 2014. – 768 с.

24. Франкл В. Плюрализм науки и единство человека // Человек в поисках смысла: Сборник. – М.: Прогресс, 1990. – С. 45–53.

25. Хайдеггер М. Вопрос о технике // Время и бытие: Статьи и выступления. – М.: Республика, 1993. – С. 221–238.

26. Шанин Н. А. Эскиз финитарного варианта математического анализа. (Препринт ПОМИ-06-2000). – СПб.: Санкт-Петербургское отделение Математического института имени В. А. Стеклова РАН, 2000.

27. Шеннон К. Математическая теория связи // Работы по теории информации и кибернетике. – М.: Издательство иностранной литературы, 1963. – С. 242–332.

28. Эшби У. Р. Схема усилителя мыслительных способностей // Автоматы. Сб. статей / Под ред. К. Э. Шеннона, Дж. Маккарти. – М.: Издательство иностранной литературы, 1956. – С. 281–305.

29. Bekenstein J. D. Black Holes and Information Theory // Contemporary Physics. 2004. – Vol. 45. – No.1. – P. 31–43.

30. Bridgman P. W. A Physicist’s Second Reaction to Mengenlehre // Scripta Mathematica. 1934. – Vol. II. – P. 101–117; 224–234.

31. Chaitin G. J. Algorithmic Information Theory // Encyclopedia of Statistical Sciences. Vol. 1. – N. Y.: Wiley, 1982. – P. 38–41.

32. Chaitin G. The Limits of Reason // Scientific American. 2006. – Vol. 294. – No. 3. – P. 74–81.

33. Chaitin G. J. Randomness and Mathematical Proof // Scientific American. 1975. – Vol. 232. – No. 5. – P. 47–52.

34. Chaitin G. J. Leibniz, Randomness and the Halting Probability // Mathematics Today. – 2004. – Vol. 40. – No. 4. – P. 138–139.

35. Chaitin G. J. Algorithmic Information Theory. – Cambridge: CambridgeUniversity Press, 1987. – 236 p.

36. Chaitin G. Meta Math! The quest for Omega. – N. Y.: Pantheon, 2005. – xix + 220 p.

37. Church A. An Unsolvable Problem of Elementary Number Theory // American Journal of Mathematic. – 1938. – Vol. 58. – No. 2. – P. 345–363.

38. Davis M. Engines of Logic. Mathematicians and the Origin of the Computer. Paperbound Reprint with Altered Title of BSL VII 65. – New York and London: W. W. Norton & Company, 2001. – xii + 257 p.

39. Der Spiegel’s Interview with Martin Heidegger // Philosophy Today. – 1967. – Vol. 20. – Issue 4 (Winter). – P. 267–284.

40. Detlefsen M., Luker M. Computer Proof // The Journal of Philosophy. – 1980. – Vol. 77. – No. 12. – P. 797–820.

41. Eriksen T. H. Tyranny of the Moment: Fast and Slow Time in the Information Age. – London; Sterling: Virginia: Pluto Press, 2001. – ix +180 p.

42. Gacs P. Review // The Journal of Symbolic Logic. – 1989. – Vol. 54. – No. 2. – P. 624–627.

43. Gacs P. Randomness and Probability – Complexity of Description // Encyclopedia of Statistical Sciences. – New York: John Wiley and Sons, 1986. Vol. 7. – P. 551–554.

44. Kahneman D. Thinking, Fast and Slow. – New York: Farrar, Straus and Giroux, 2011. – 500 p.

45. Landauer R. Irreversibility and Heat Generation in the Computing Process // IBM Journal of Research and Development. – 1961. – Vol. 5. – Iss. 3. – P. 183–191.

46. Landauer R. Wanted: A Physically Possible Theory of Physics // IEEE Spectrum. – 1967. – Vol. 4. – No. 9. – P. 105–109.

47. Landauer R. Uncertainty Principle and Minimal Energy Dissipation in the Computer // International Journal of Theoretical Physics. – 1982. – Vol. 21. – Nos. 3/4. – P. 283–297.

48. Landauer R. Fundamental Physical Limitations of the Computational Process // Annals of the New YorkAcademy of Sciences. – 1984. – Vol. 246. – Iss. 1. – P. 161–170.

49. Landauer R. Computation and Physics: Wheeler’s Meaning Circuit? // Foundations of Physics. – 1986. – Vol. 16. – No. 6. – P. 551–564.

50. Landauer R. Wheeler’s Meaning Circuit? // Foundations of Physics. – 1986. – Vol. 16. – No. 6. – P. 551–564.

51. Landauer R. Dissipation and Noise Immunity in Computation and Communication // Nature. – 1988. – Vol. 335. – P. 779–784.

52. Landauer R. Computation: A Fundamental Physical View // Physica Scripta. – 1987. – Vol. 35. – No. 1. – P. 88–95.

53. Landauer R. Minimal Energy Requirements in Communication // Science. – 1996. – Vol. 272. – № 5270. – P. 1914–1918.

54. Landauer R. The Physical Nature of Information // Physics Letters. A. – 1996. – Vol. 217. – Iss. 4–5. – P. 188–193.

55. Lewis J. P. Large Limits to Software Estimation // ACM Software Engineering Nots. – 2001. – Vol. 26. – No. 4. – P. 54–59.

56. Li M., Vitanyi P. An Introduction to Kolmogorov Complexity and Its Applications. – New York: Springer, 1993. – 566 p.

57. Lloyd S., Giovannetti V., Maccone L. Physical Limits to Communication // Physical Review Letters. – 2004. – Vol. 93. – No. 10. – P. 100501-1–100501-4.

58. Mavran M. The Energy Dissipation, the Error Probability and the Time of Duration of a Logical Operation // Kybernetika. – 1982. – Vol. 18. – No. 4. – P. 345–355.

59. Nielsen M. A., Chuang I. L. Quantum Computation and Quantum Information. – Cambridge: CambridgeUniversity Press, 2000. – 676 p.

60. Nilsson N. Artificial Intelligence: A New Synthesis. – San Francisco: Morgan Kaufmann, 1998. – 513 p.

61. Raatikainen P. «Exploring Randomness» and «The Unknowable» // The Notices of the American Mathematical Society. – 2001. – Vol. 48. – No. 9. – P. 992–996.

62. Shanin N. A. On a Finitary Version of Mathematical Analysis // Annals of Pure and Applied Logic. – 2002. – Vol. 113. – Iss. 1–3. – P. 261–295.

63. Shannon C. E. The Mathematical Theory of Communication // Bell System Technology Journal. – 1948. – Vol. 27. – No. 3. – P. 379–423.

64. Shannon C. E. The Mathematical Theory of Communication // Bell System Technology Journal. – 1948. – Vol. 27. – No. 4. – P. 623–656.

65. Solomonoff R. A Formal Theory of Inductive Inference. Part I // Information and Control. – 1964. – Vol. 7. – No. 1. – P. 1–22.

66. Taleb N. N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets. – New York: Random House, 2004. – xlviii + 320 p.

67. Taleb N. N. The Black Swan: The Impact of the Highly Improbable. – New York: Random House, 2007. – xxxiii + 445 p.

68. Taleb N. N. Antifragile: Things That Gain from Disorder. – New York: Random House, 2012. – xxi + 521 p.

69. Turing A. On Computable Numbers with Applications to Entscheidungsproblem // Proceedings of the London Mathematical Society. – 1936. –1937. – Ser. 2. – Vol. 42. – P. 230–265.

70. Tymoczko T. The Four-Color Problem and Its Philosophical Significance // The Journal of Philosophy. – 1979. – Vol. 76. – No. 2. – P. 57–83.

 

References

1. Conversation of Employees of the Magazine “Der Spiegel” R. Augstein and G. Wolf with M. Heidegger on September 23, 1966 [Beseda sotrudnikov zhurnala “Shpigel” R. Augshtayna i G. Volfa s Martinom Haydeggerom 23 sentyabrya 1966 g.]. Filosofiya Martina Hajdeggera i sovremennost (Martin Heidegger’s Philosophy and Modernity). Moscow, Nauka, 1991, pp. 233–250.

2. Boolos G., Jeffrey R. Computability and Logic [Vychislimost i logika]. Moscow, Mir, 1994, 400 p.

3. Gardner H. The Structure of Mind: The Theory of Multiple Intelligence [Structura razuma, teoria mnozhestvennogo intellekta]. Moscow, “I. D. Vilams”, 2007, 512 p.

4. Hegel G. V. F. Encyclopedia of Philosophical Sciences. Part one. Logic [Enciklopediya filosofskikh nauk. Chast pervaya. Logika]. Sochineniya, T. I (Works, Vol. 1). Moscow-Leningrad, Gosudarstvennoe izdatelstvo, 1929, 368 p.

5. Homer. Iliad [Iliada]. Iliada. Odisseya (Iliad. Odyssey). Moscow, Gosudarstvennoe izdatelstvo “Khudozhestvennaya literature”, 1967, 767 p.

6. Zvonkin A. K., Levin L. A. The Complexity of Finite Objects and the Justification of the Concepts of Information and Randomness by Means of the Theory of Algorithms [Slozhnost konechnykh obektov i obosnovanie ponyatiya informacii i sluchaynosti s pomoschyu teorii algoritmov]. Uspekhi matematicheskikh nauk (Successes of Mathematical Sciences), Vol. 25, Iss. 6, Moscow, AN SSSR, 1970, p. 85–127.

7. Kahneman D. Think Slowly… Solve Quickly [Dumai medlenno… reshai bistro]. Moscow, AST, 2014, 654 p.

8. Karavaev E. F. Modern Considerations of the Thesis of Church-Turing [Sovremennye rassmotreniya tezisa Chercha-T'yuringa]. Vestnik Sankt-Peterburgskogo universiteta [Bulletin of St. Petersburg University], Series 6, Philosophy, Political Science, Sociology, Psychology, Law, 1996, Iss. 2 (No. 13), pp. 28–33.

9. Karavaev E. F. Formalization Is a Tool Developed by Logic for Scientific Knowledge [Formalizaciya – instrument, razrabatyvaemyy logikoy dlya nauchnogo poznaniya]. Vestnik Sankt-Peterburgskogo universiteta [Bulletin of St. Petersburg University], Series 6, Philosophy, Political Science, Sociology, Psychology, Law. 1999, Iss. 2 (No. 13), pp. 3–10.

10. Karavaev E. F., Nikitin V. E. Topological Means of Taking into Account Chance in the Socio-Cultural Analysis of Technological Development [Topologicheskie i metricheskie sredstva uchyota sluchaynosti v sociokulturnom analize tekhnologicheskogo razvitiya]. Kontury buduschego: tekhnologii i innovacii v kulturnom kontekste. Kollektivnaya monografiya. [The Contours of the Future: Technology and Innovations in a Cultural Context. Collective Monograph]. D. I. Kuznetsov, V. V. Sergeeva, N. V. Almazova, N. V. Nikiforova (Eds.) Saint Petersburg, Asterion, 2017, pp.113–116.

11. Karavaev E. F., Nikitin V. E. Synergetic Philosophy of History, Chance, Logic, Time [Sinergeticheskaya filosofiya istorii, sluchajnost, logika, vremya]. Filosofiya i gumanitarnye nauki v informacionnom obschestve [Philosophy and Humanities in the Information Society], 2018. No.1 (19), pp.12–32. Available at: http://fikio.ru/?p=3088 (accessed 30 September 2018).

12. Kolmogorov A. N. Three Approaches to the Definition of “Amount of Information” [Tri podhoda k opredeleniyu ponyatiya “kolichestvo informacii”]. Problemy peredachi informacii (Problems of Information Transmission), Vol. 1, No. 1, Moscow, Nauka, 1965, pp. 3–11.

13. Kolmogorov A. N. On the Logical Foundations of Information Theory and Probability Theory [K logicheskim osnovam teorii informacii i teorii veroyatnostey]. Problemy peredachi informacii (Problems of Information Transmission), Vol. 5, No. 3, Moscow, Nauka, 1969, pp. 3–7.

14. Leibniz G.-W. Discourse on Metaphysics [Rassuzhdenie o metafizike]. Sochineniya. Tom I (Works. Vol. I). Moscow, Mysl, 1982, pp. 125–163.

15. Leibniz G.-W. Beginnings of Nature and Grace Based on Reason [Nachala prirody i blagodati, osnovannye na razume]. Sochineniya. Tom I (Works. Vol. I). Moscow, Mysl, 1982, p. 404–412.

16. Leibniz G.-W. Monadology [Monadologiya]. Sochineniya. Tom I (Works. Vol. I). Moscow, Mysl, 1982, p. 413–439.

17. Marx K. Economic Manuscripts of 1857–1859 [Ekonomicheskie rukopisi 1857–1859 godov]. Marx K., Engels F. Sochineniya. Tom 46. Part II (Works. Vol. 46. Part II). Moscow, Polinizdat, 1968, 618 p.

18. Riemann B. On the Hypothesis Lying at the Foundation of Geometry [O gipotezah, lezhaschih v osnovanii geometrii]. Sochineniya (Works). Moscow-Leningrad, Ogiz, Gosudarstvennoe izdatelstvo tekhniko-teoreticheskoy literatury, 1948, pp. 279–293.

19. Safranski R. Nietzsche: A Biography of His Mind [Nicshe: biografiya ego mysli]. Moscow, Izdatelskiy dom “Delo” RANHiGS, 2016, 456 p.

20. Styazhkin N. I. Formation of Mathematical Logic [Formirovanie matematicheskoy logiki]. Moscow, Nauka, 1967, 508 p.

21. Taleb N. N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets [Odurachennye sluchajnostyu. Skrytaya rol shansa v biznese i zhizni]. Moscow, Mann, Ivanov i Ferber, 2011, 320 p.

22. Taleb N. N. The Black Swan: The Impact of the Highly Improbable [Chernyy lebed. Pod znakom nepredskazuemosti]. Moscow, KoLibri, Azbuka-Attikus, 2011, 528 p.

23. Taleb N. N. Antifragile: Things That Gain from Disorder [Antikhrupkost. Kak izvlech vygodu iz haosa]. Moscow, KoLibri, Azbuka-Attikus, 2014, 768 p.

24. Frankl V. The Pluralism of Science and Unity of Man [Plyuralizm nauki i edinstvo cheloveka]. Chelovek v poiskah smysla: Sbornik (Man in Search of Meaning: Collected Works). Moscow, Progress, 1990, pp. 45–53.

25. Heidegger M. A Question of Technique [Vopros o tekhnike]. Vremya i byte: Stati i vystupleniya (Time and Being: Articles and Speeches). Moscow, Respublika, 1993, pp. 221–238.

26. Shanin N. A. A Sketch of Finitary Variant of Mathematical Analysis [Eskiz finitarnogo varianta matematicheskogo analiza]. (Preprint POMI-06-2000). Saint Petersburg, Sankt-Peterburgskoe otdelenie Matematicheskogo instituta imeni V. A. Steklova RAN, 2000.

27. Shannon C. Mathematical Theory of Communication [Matematicheskaya teoriya svyazi]. Raboty po teorii informacii i kibernetike (Works on Information Theory and Cybernetics). Moscow, Izdatelstvo inostrannoy literatury, 1963, pp. 242–332.

28. Ashby W. R. The Scheme of the Amplifier of Mental Abilities [Skhema usilitelya myslitelnykh sposobnostey]. Automata. Collected Articles (Avtomaty. Sbornik statey). Ed. by C. E. Shannon, J. McCarthy. Moscow, Izdatelstvo inostrannoy literatury, 1956, pp. 281–305.

29. Bekenstein J. D. Black Holes and Information Theory. Contemporary Physics, 2004, Vol. 45, No. 1, pp. 31–43.

30. Bridgman P. W. A Physicist’s Second Reaction to Mengenlehre. Scripta Mathematica, 1934, Vol. II, pp. 101–117, 224–234.

31. Chaitin G. J. Algorithmic Information Theory. Encyclopedia of Statistical Sciences. Vol. 1. N. Y., Wiley, 1982, pp. 38–41.

32. Chaitin G. The Limits of Reason. Scientific American, 2006, Vol. 294, No. 3, pp. 74–81.

33. Chaitin G. J. Randomness and Mathematical Proof. Scientific American, 1975, Vol. 232, No. 5, pp. 47–52.

34. Chaitin G. J. Leibniz, Randomness and the Halting Probability. Mathematics Today, 2004, Vol. 40, No. 4, pp. 138–139.

35. Chaitin G. J. Algorithmic information theory. Cambridge, CambridgeUniversity Press, 1987, 236 p.

36. Chaitin G. Meta Math! The Quest for Omega. N. Y., Pantheon, 2005, xix + 220 p.

37. Church A. An Unsolvable Problem of Elementary Number Theory. American Journal of Mathematics, 1938, Vol. 58, No. 2, pp. 345–363.

38. Davis M. Engines of logic. Mathematicians and the origin of the computer. Paperbound reprint with altered title of BSL VII 65. New York and London, W. W. Norton & Company, 2001, xii + 257 p.

39. Der Spiegel’s Interview with Martin Heidegger. Philosophy Today, 1967, Vol. 20, Issue 4 (Winter), pp. 267–284.

40. Detlefsen M., Luker M. Computer Proof. The Journal of Philosophy, 1980, Vol. 77, No.12, pp. 797–820.

41. Eriksen T. H. Tyranny of the Moment: Fast and Slow Time in the Information Age. London; Sterling, Virginia, Pluto Press, 2001, – ix +180 p.

42. Gacs P. Review. The Journal of Symbolic Logic, 1989, Vol. 54, No. 2, pp. 624–627.

43. Gacs P. Randomness and Probability – Complexity of Description. Encyclopedia of Statistical Sciences. N. Y., John Wiley and Sons, 1986, Vol. 7, pp. 551–554.

44. Kahneman D. Thinking, fast and slow. New York, Farrar, Straus and Giroux, 2011, 500 p.

45. Landauer R. Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development, 1961, Vol. 5, Iss. 3, pp. 183–191.

46. Landauer R. Wanted: A Physically Possible Theory of Physics. IEEE Spectrum, 1967, Vol. 4, No. 9, pp. 105–109.

47. Landauer R. Uncertainty Principle and Minimal Energy Dissipation in the Computer. International Journal of Theoretical Physics, 1982, Vol. 21, Nos. ¾, pp. 283–297.

48. Landauer R. Fundamental Physical Limitations of the Computational Process. Annals of the New York Academy of Sciences, 1984, Vol. 246, Iss. 1, pp. 161–170.

49. Landauer R. Computation and Physics: Wheeler’s Meaning Circuit? Foundations of Physics, 1986, Vol. 16, No. 6, pp. 551–564.

50. Landauer R. Dissipation and Noise Immunity in Computation and Communication. Nature, 1988, Vol. 335, pp. 779–784.

51. Landauer R. Computation: A Fundamental Physical View. Physica Scripta, 1987, Vol. 35, No. 1, pp. 88–95.

52. Landauer R Information is Physical. Physics Today, 1991, Vol. 44, Iss. 5, pp. 23–29.

53. Landauer R. Minimal Energy Requirements in Communication. Science, 1996, Vol. 272, № 5270, pp. 1914–1918.

54. Landauer R. The Physical Nature of Information. Physics Letters. A, 1996, Vol. 217, Iss. 4–5, pp. 188–193.

55. Lewis J. P. Large Limits to Software Estimation. ACM Software Engineering Nots, 2001, Vol. 26, No. 4, pp. 54–59.

56. Li M., Vitanyi P. An Introduction to Kolmogorov Complexity and Its Applications. N. Y., Springer, 1993, 566 p.

57. Lloyd S., Giovannetti V., Maccone L. Physical Limits to Communication. Physical Rreview Letters, 2004, Vol. 93, No. 10, pp. 100501-1–100501-4.

58. Mavran M. The Energy Dissipation, the Error Probability and the Time of Duration of a Logical Operation. Kybernetika, 1982, Vol. 18, No.4, pp. 345–355.

59. Nielsen M. A., Chuang I. L. Quantum Computation and Quantum Information. Cambridge, CambridgeUniversity Press, 2000, 676 p.

60. Nilsson N. Artificial Intelligence: A New Synthesis. San Francisco, Morgan Kaufmann, 1998, 513 p.

61. Raatikainen P. “Exploring Randomness” and “The Unknowable”. The Notices of the American Mathematical Society, 2001, Vol. 48, No. 9, pp. 992–996.

62. Shanin N. A. On a Finitary Version of Mathematical Analysis. Annals of Pure and Applied Logic, 2002, Vol. 113, Iss.1–3, pp. 261–295.

63. Shannon C. E. The Mathematical Theory of Communication. Bell System Technology Journal, 1948, Vol. 27, No. 3, pp. 379–423.

64. Shannon C. E. The Mathematical Theory of Communication. Bell System Technology Journal, Vol. 27, No. 4, pp. 623–656.

65. Solomonoff R. A Formal Theory of Inductive Inference. Part I. Information and Control, 1964, Vol. 7, No. 1, pp. 1–22.

66. Taleb N. N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets. New York, Random House, 2004, xlviii + 320 p.

67. Taleb N. N. The Black Swan: The Impact of the Highly Improbable. New York, Random House, 2007, xxxiii + 445 p.

68. Taleb N. N. Antifragile: Things That Gain from Disorder. New York, Random House, 2012, xxi + 521 p.

69. Turing A. On Computable Numbers with Applications to Entscheidungsproblem. Proceedings of the London Mathematical Society, 1936–1937, Ser. 2, Vol. 42, pp. 230–265.

70. Tymoczko T. The Four-Color Problem and Its Philosophical Significance. The Journal of Philosophy, 1979, Vol. 76, No. 2, pp. 57–83.